题目内容
经过市场调查发现,某商品在60天内的日销售价和日销售量都是时间x(天)的一次函数,其中2天的销售价和销售量如下表所示:
(1)写出该商品的日销售价f(x)和日销售量g(x)与时间x的函数表达式;
(2)求日销售额y(元)与时间的函数关系式,并求出日销售额最高的是哪一天?最高日销售额是多少?(日销售额=日销售价×日销售量)
| 时间x(天) | 第12天 | 第36天 |
| 日销售价f(x)(元/件) | 36 | 28 |
| 日销售量g(x)(件) | 18 | 24 |
(2)求日销售额y(元)与时间的函数关系式,并求出日销售额最高的是哪一天?最高日销售额是多少?(日销售额=日销售价×日销售量)
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)根据一次函数的性质利用待定系数法求出函数解析式即可;
(2)利用W=销量×每件商品利润,进而结合二次函数最值求法得出即可.
(2)利用W=销量×每件商品利润,进而结合二次函数最值求法得出即可.
解答:
解:(1)∵某商品在60天内的日销售价和日销售量都是时间x(天)的一次函数,
∴设f(x)=kx+b,代入(12,36),(36,28),可得k=-
,b=40,
设g(x)=mx+n,代入(12,36),(36,28),可得m=
,n=15,
∴f(x)=-
x+40,g(x)=
x+15,(1≤x≤60,x∈N*)…(4分)
(2)当1≤x≤60,x∈N*时【注:(1)中定义域错扣(1分)】y=f(x)•g(x)=(-
x+40)(
x+15)=-
x2+5x+600…(5分)
=-
(x-30)2+675…(6分)
∴当x=30时,y有最大值675.…(7分)
∴日销售额最高的是第30天,最高销售额是675元.…(8分)
∴设f(x)=kx+b,代入(12,36),(36,28),可得k=-
| 1 |
| 3 |
设g(x)=mx+n,代入(12,36),(36,28),可得m=
| 1 |
| 4 |
∴f(x)=-
| 1 |
| 3 |
| 1 |
| 4 |
(2)当1≤x≤60,x∈N*时【注:(1)中定义域错扣(1分)】y=f(x)•g(x)=(-
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
=-
| 1 |
| 12 |
∴当x=30时,y有最大值675.…(7分)
∴日销售额最高的是第30天,最高销售额是675元.…(8分)
点评:此题主要考查了二次函数的应用以及二次函数的性质以及待定系数法求一次函数解析式等知识,利用二次函数的性质得出x的取值范围是解题关键.

练习册系列答案
相关题目
 一个圆锥的底面半径为2cm,高为6cm,在圆锥内部有一个高为xcm的内接圆柱.(如图为轴截面图)
一个圆锥的底面半径为2cm,高为6cm,在圆锥内部有一个高为xcm的内接圆柱.(如图为轴截面图)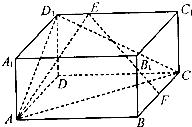 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).