题目内容
3.随着手机的发展,“微信”逐渐成为人们交流的一种形式,某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频率分布及“使用微信交流”赞成人数如下表.| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据统计数据,可得2×2列联表,根据列联表中的数据,计算K2的值,即可得到结论;
(2)利用对立事件的概率公式,即可求2人中至少有1人不赞成“使用微信交流”的概率.
解答 解:(1)由以上统计数据填写下面 2×2 列联表,如下;
| 年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
| 赞成 | 10 | 27 | 37 |
| 不赞成 | 10 | 3 | 13 |
| 合计 | 20 | 30 | 50 |
所以有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
(2)设年龄在[55,65)中不赞成“使用微信交流”的人为A、B、C,赞成“使用微信交流”的人为a,b,
则从5人中随机选取2人有AB,AC,Aa,Ab,BC,Ba,Bb,Ca,Cb,ab,10个结果;其中2人中至少有1人不赞成“使用微信交流”的有AB,AC,Aa,Ab,BC,Ba,Bb,Ca,Cb,9个结果,所以2人中至少有1人不赞成“使用微信交流”的概率为$P=\frac{9}{10}$.
点评 本题考查独立性检验,考查古典概型的概率的计算,考查学生的阅读与计算能力,属于基础题.

练习册系列答案
相关题目
13.已知直线x=$\frac{b}{2}$与椭圆C:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0)交于A、B两点,若椭圆C的两个焦点与A、B两点可以构成一个矩形,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{10}}{4}$ |
14.设倾斜角为α的直线l经过抛物线C:y2=2px(p>0)的焦点F,与抛物线C交于A,B两点,设点A在x轴上方,点B在x轴下方.若$\frac{|AF|}{|BF|}=m$,则cosα的值为( )
| A. | $\frac{m-1}{m+1}$ | B. | $\frac{m}{m+1}$ | C. | $\frac{m-1}{m}$ | D. | $\frac{{2\sqrt{m}}}{m+1}$ |
8.已知等比数列{an}的前n项和为Sn,则“a1>0”是“S2017>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
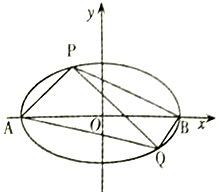 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.