题目内容
3．
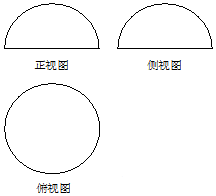如图是一个几何体的三视图，正视图、侧视图是半径为R的半圆，俯视图是半径为R的圆，若该几何体的表面积为6π，则R=（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{6}$ |
分析 由三视图知几何体为半球，利用几何体的表面积为6π，即可计算R．
解答 解：由三视图知几何体为半球，则
∵该几何体的表面积为6π，
∴$\frac{1}{2}×4π$×R3=6π，
∴R=$\sqrt{3}$．
故选：B．
点评 本题考查了由三视图求几何体的表面积，考查了球的表面积公式，解题的关键是判断几何体的形状及数据所对应的几何量．
练习册系列答案
相关题目
15．从已有3个红球、2个白球的袋中任取3个球，设A={至少取到两个红球}，B={恰好取到一个白球}，则事件AB的概率是（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{3}{10}$ | C． | $\frac{3}{5}$ | D． | $\frac{9}{10}$ |
12．下列说法错误的是（ ）
| A． | 命题“若x2-4x+3=0，则x=3或x=1”的逆否命题是“若x≠3且x≠1，则x2-4x+3=0≠0” | |
| B． | “x2-x=0”是“x=1”的必要不充分条件 | |
| C． | 若p∨q为真命题，则p，q均为真命题 | |
| D． | 命题p：?x∈R，使得x3+x+1=0，则￢p：?x∈R，使得x3+x+1≠0 |