题目内容
14.平面四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一个球面上,则该球的表面积3π.分析 由题意,BC的中点就是球心,求出球的半径,即可得到球的表面积.
解答 解:由题意,四面体A-BCD顶点在同一个球面上,△BCD和△ABC都是直角三角形,
所以BC的中点就是球心,所以BC=$\sqrt{3}$,球的半径为:$\frac{\sqrt{3}}{2}$
所以球的表面积为:$4π•(\frac{\sqrt{3}}{2})^{2}$=3π.
故答案为:3π.
点评 本题是基础题,考查四面体的外接球的表面积的求法,找出外接球的球心,是解题的关键,考查计算能力,空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在正方体A'C中,D'A与BD所成的角的度数为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
6.点P在曲线C:$\frac{x^2}{4}+{y^2}$=1上,若存在过点P的直线交曲线C于A点,交直线l:x=4于B点,且满足|PA|=|PB|,则称P点为“二中点”,那么下列结论正确的是( )
| A. | 曲线C上的所有点都是“二中点” | |
| B. | 曲线C上的仅有有限个点是“二中点” | |
| C. | 曲线C上的所有点都不是“二中点” | |
| D. | 曲线C上的有无穷多个点(但不是所有的点)是“二中点” |
3.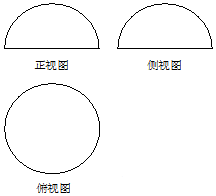 如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )
如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )
 如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )
如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |