题目内容
13．已知函数f（x）=2x3-3（a+1）x2+bx．（1）若曲线y=f（x）在点（2，f（2））处的切线方程为y=6x-8，求实数a、b的值；
（2）若b=6a，a＞1，求f（x）在闭区间[0，4]上的最小值．
分析 （1）求出函数的导数，计算f′（2），f（2）的值，求出a，b的值即可；
（2）求出函数的导数，解关于导函数的不等式，通过讨论a的范围求出函数的最小值即可．
解答 解：（1）切线方程为y=6x-8，f′（x）=6x2-6（a+1）x+b，
所以f′（2）=6，又因为f（2）=4，解得：a=1，b=6．
（2）记g（a）为 f（x）在闭区间[0，4]上的最小值，
f′（x）=6（x-1）（x-a），
令f′（x）=0，得到x=1或a，
当1＜a＜4时，
| x | 0 | （0，1） | 1 | （1，a） | a | （a，4） | 4 |
| f′（x） | + | 0 | - | 0 | + | ||
| f（x） | 0 | 单调 递增 | 极大值 3a-1 | 单调 递减 | 极小值 a2（3-a） | 单调 递增 | 80-24a |
g（a）=$\left\{\begin{array}{l}{0，1＜a≤3}\\{{a}^{2}（3-a），3＜a＜4}\end{array}\right.$
当a≥4时，
| x | 0 | （0，1） | 1 | （1，4） | 4 |
| f′（x） | + | 0 | - | ||
| f（x） | 0 | 单调 递增 | 极大值 3a-1 | 单调 递减 | 80-24a |
综上所述，f（x）在闭区间[0，4]上的最小值为
g（a）=$\left\{\begin{array}{l}{0，1＜a≤3}\\{{a}^{2}（3-a），3＜a＜4}\\{80-24a，a≥4}\end{array}\right.$．
点评 本题考查了切线方程问题，考查函数的单调性、最值问题，考查导数的应用以及分类讨论思想，是一道中档题．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
3．
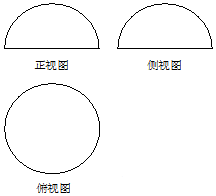如图是一个几何体的三视图，正视图、侧视图是半径为R的半圆，俯视图是半径为R的圆，若该几何体的表面积为6π，则R=（ ）
如图是一个几何体的三视图，正视图、侧视图是半径为R的半圆，俯视图是半径为R的圆，若该几何体的表面积为6π，则R=（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{6}$ |
18．如图所示的算法流程图中，第3个输出的数是（ ）
| A． | 1 | B． | 2 | C． | $\frac{3}{2}$ | D． | $\frac{5}{2}$ |
如图所示，已知⊙O的半径是1，点C在直径AB的延长线上，BC=1，点P是⊙O上半圆上的一个动点，以PC为边作等边三角形PCD，且点D与圆心分别在PC的两侧．