题目内容
15.已知a,b都是正实数,且满足log9(9a+b)=log3$\sqrt{ab}$,则3a+b的最小值为12+6$\sqrt{3}$.分析 先根据条件得出$\frac{1}{a}+\frac{9}{b}$=1,再根据单位1,即贴1法求和基本不等式求函数的最小值.
解答 解:∵${log_9}(9a+b)={log_3}\sqrt{ab}$,
∴9a+b=ab,即$\frac{1}{a}+\frac{9}{b}$=1,
所以,3a+b=(3a+b)•1
=(3a+b)•($\frac{1}{a}+\frac{9}{b}$)
=3+9+$\frac{b}{a}$+$\frac{27a}{b}$
≥12+2•$\sqrt{\frac{b}{a}•\frac{27a}{b}}$=12+6$\sqrt{3}$,
当且仅当:a=1+$\sqrt{3}$,b=3(3+$\sqrt{3}$)时,取“=”,
即3a+b的最小值为:12+6$\sqrt{3}$,
故答案为:12+6$\sqrt{3}$.
点评 本题主要考查了基本不等式在求最值问题中的应用,涉及对数的运算和“贴1法”的灵活运用,属于中档题.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
5.设集合A={0,1,2,4},B=$\left\{{\left.{x∈R|\frac{x-4}{x-2}≤0}\right\}}$,则A∩B=( )
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {4} | D. | {x|1<x≤4} |
3.已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
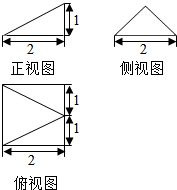

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | 2 |
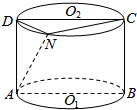 如图,已知矩形ABCD是圆柱O1O2的轴截面,N在上底面的圆周O2上,AC、BD相交于点M;
如图,已知矩形ABCD是圆柱O1O2的轴截面,N在上底面的圆周O2上,AC、BD相交于点M;