题目内容

10．设等差数列{an}的前n项的和为Sn，且满足S2014＞0，S2015＜0，对任意正整数n，都有|an|≥|ak|，则k的值为1008．

分析 由等差数列的求和公式和性质可得a1007＞0，a1008＜0，且|a1007|＞|a1008|，由题意易得结论．

解答 解：由等差数列的求和公式和性质可得S2014=$\frac{2014{（a}_{1}+{a}_{2014}）}{2}$=1007（a1007+a1008）＞0，
∴a1007+a1008＞0
同理由S2015＜0可得2015a1008＜0，可得a1008＜0，
∴a1007＞0，a1008＜0，且|a1007|＞|a1008|
∵对任意正整数n，都有|an|≥|ak|，
∴k的值为1008，
故答案为：1008．

点评 本题考查等差数列的性质和求和公式，得出数列的最小项是解决问题的关键，属基础题

练习册系列答案
相关题目
20．$\root{6}{（a-b）^{6}}$（a＜b）=b-a．
1．已知函数$f（x+\frac{1}{2}）$为奇函数，g（x）=f（x）+1，若${a_n}=g（\frac{n}{2016}）$，则数列的前2015项之和为（　　）
A．2016B．2015C．2014D．2013
18．已知直线l：$\left\{\begin{array}{l}{x=1+\sqrt{3}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$（t为参数），曲线C1：$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）．
（1）设l与C1相交于A，B两点，求|AB|；
（2）若把曲线C1上各点的横坐标压缩为原来的$\frac{1}{2}$，纵坐标压缩为原来的$\frac{{\sqrt{3}}}{2}$得到曲线C2，设点P是曲线C2上的一个动点，求它到直线l的距离的最大值．
5．函数f（x）=lnx-|x-2|的零点的个数为2．
15．已知a，b都是正实数，且满足log9（9a+b）=log3$\sqrt{ab}$，则3a+b的最小值为12+6$\sqrt{3}$．
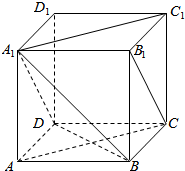2．如图在正方体ABCD-A1B1C1D1中，
（1）求证：平面AA1C1C⊥平面A1BD
（2）求直线A1B与平面A1B1CD所成的角．
19．（理）下列四个命题中真命题的序号是①③．
①若存在实数x，y，使$\overrightarrow p=x\overrightarrow a+y\overrightarrow b$，则$\overrightarrow P$与$\overrightarrow a，\overrightarrow b$共面；
②若$\overrightarrow P$与$\overrightarrow a，\overrightarrow b$共面，则存在实数x，y，使$\overrightarrow p=x\overrightarrow a+y\overrightarrow b$；
③若存在实数x，y，使$\overrightarrow{MP}=x\overrightarrow{MA}+y\overrightarrow{MB}$，则P，M，A，B共面；
④若P，M，A，B共面，则存在实数x，y，使$\overrightarrow{MP}=x\overrightarrow{MA}+y\overrightarrow{MB}$．
20．已知直线m过双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的左焦点F1，且与该双曲线的左支交于A，B两点，若|AB|=2，双曲线的右焦点为F2，则△ABF2的周长为（　　）
A．6B．8C．12D．20

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网