题目内容
7.已知函数f(x)=$\sqrt{4-x}+{log_3}$(x-2)的定义域为集合A,函数$g(x)={log_2}x,(\frac{1}{4}≤x≤8)$的值域为集合B.(1)求A∪B;
(2)若集合C={x|a≤x≤3a-1},且B∩C=C,求实数a的取值范围.
分析 (1)先求出集合A={x|2<x≤4},B={x|-2≤x≤3},再直接取它们的并集;
(2)问题等价为C⊆B,再对集合C分类讨论,得出实数a的取值范围.
解答 解(1)函数f(x)的自变量x需满足条件$\left\{\begin{array}{l}{4-x≥0}\\{2-x>0}\end{array}\right.$,
解得,2<x≤4,所以,A={x|2<x≤4},
对于函数g(x),因为$\frac{1}{4}$≤x≤8,
所以,g(x)=log2x∈[-2,3],
因此,B={x|-2≤x≤3},
所以,A∪B={x|-2≤x≤4};
(2)由B∩C=C得,C⊆B,对集合C讨论如下:
①当C=∅时,a>3a-1,解得a<$\frac{1}{2}$,
因为空集是任何集合的子集,故符合题意;
②当C≠∅时,需要满足下列条件:
$\left\{\begin{array}{l}{a≤3a-1}\\{a≥-2}\\{3a-1≤3}\end{array}\right.$,解得,$\frac{1}{2}$≤a≤$\frac{4}{3}$,
综合以上讨论得,实数a的取值范围为:(-∞,$\frac{4}{3}$].
点评 本题主要考查了交集及其运算,对数函数的图象与性质,以及空集的性质,体现了分类讨论的解题思想,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
17.f(x)=sin(x+θ),|θ|<$\frac{π}{2}$,函数图象向右平移$\frac{π}{3}$个单位后得到的函数为奇函数,则θ值等于( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{6}$ |
16.已知双曲线$\frac{x^2}{a^2}\;-\;\frac{y^2}{b^2}\;=\;1\;({a>0,b>0})$与圆${x^2}+{y^2}\;={c^2}\;({c\;=\sqrt{{a^2}+{b^2}}})$交于A、B、C、D四点,若四边形ABCD是正方形,则双曲线的离心率是( )
| A. | $\sqrt{2+\sqrt{2}}$ | B. | $\sqrt{2+2\sqrt{2}}$ | C. | $\sqrt{1+\sqrt{2}}$ | D. | $\sqrt{1+2\sqrt{2}}$ |
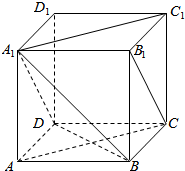 如图在正方体ABCD-A1B1C1D1中,
如图在正方体ABCD-A1B1C1D1中,