题目内容
5.用数学归纳法证明斐波拉契数列的通项公式.分析 验证n=1、2时命题成立,然后假设对一般的n=1,2,3,4,…k时命题成立,由归纳假设,结合ak+1=ak+ak-1,证明n=k+1时命题成立.
解答 证明:${a}_{n}=\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]$.
当n=1时,${a}_{1}=\frac{1}{\sqrt{5}}[\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2}]=1$,
当n=2时,${a}_{2}=\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{2}-(\frac{1-\sqrt{5}}{2})^{2}]$=$\frac{1}{\sqrt{5}}[\frac{6+2\sqrt{5}}{4}-\frac{6-2\sqrt{5}}{4}]=1$;
假设对一般的n=1,2,3,4,…k时命题成立,那么当n=k+1时:
ak+1=ak-1+ak=$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{k-1}-(\frac{1-\sqrt{5}}{2})^{k-1}]$$+\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{k}-(\frac{1-\sqrt{5}}{2})^{k}]$
=$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{k-1}(1+\frac{1+\sqrt{5}}{2})-(\frac{1-\sqrt{5}}{2})^{k-1}(1+\frac{1-\sqrt{5}}{2})]$
=$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{k-1}•\frac{3+\sqrt{5}}{2}-(\frac{1-\sqrt{5}}{2})^{k-1}•\frac{3-\sqrt{5}}{2}]$
=$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{k-1}(\frac{1+\sqrt{5}}{2})^{2}-(\frac{1-\sqrt{5}}{2})^{k-1}(\frac{1-\sqrt{5}}{2})^{2}]$
=$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{k+1}-(\frac{1-\sqrt{5}}{2})^{k+1}]$.
综上,命题对于任意的n∈N*都成立.
即斐波拉契数列的通项公式为${a}_{n}=\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]$.
点评 本题考查数学归纳法证明数列不等式,证明该题的关键是保证基础,即需验证n=1、2成立,是中档题.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. | $\sqrt{2+\sqrt{2}}$ | B. | $\sqrt{2+2\sqrt{2}}$ | C. | $\sqrt{1+\sqrt{2}}$ | D. | $\sqrt{1+2\sqrt{2}}$ |
| A. | 6 | B. | 8 | C. | 12 | D. | 20 |
| A. | f(0)<f(-3)+f(2) | B. | f(0)=f(-3)+f(2) | C. | f(0)>f(-3)+f(2) | D. | 不确定 |
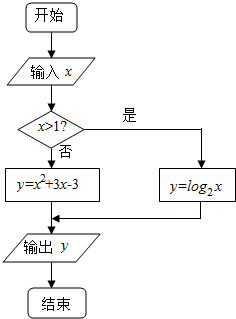
| A. | (-4,2]∪[2,+∞) | B. | [-4,1]∪[2,+∞) | C. | [-4,-2]∪{1}∪[4,+∞) | D. | (-∞,-4]∪{1}∪[2,+∞) |
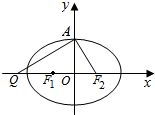 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交z轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}$+$\overrightarrow{{F_2}Q}$=$\overrightarrow{0}$,若过A,Q,F2三点的圆的半径为2.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交z轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}$+$\overrightarrow{{F_2}Q}$=$\overrightarrow{0}$,若过A,Q,F2三点的圆的半径为2.