题目内容
15. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB是直角,AB∥CD,AD=CD=2AB=2,E、F分别为PC、CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB是直角,AB∥CD,AD=CD=2AB=2,E、F分别为PC、CD的中点.(Ⅰ)试证:AB⊥平面BEF;
(Ⅱ)若VC-BEF=1,求PA的长.
分析 (Ⅰ)欲证AB⊥平面BEF,根据直线与平面垂直的判定定理可知只需证AB与平面BEF内两相交直线垂直,而AB⊥BF.根据面面垂直的性质可知AB⊥EF,满足定理所需条件;
(Ⅱ)利用体积公式,结合VC-BEF=1,求PA的长.
解答 (Ⅰ)证明:由已知DF∥AB且∠DAB为直角,
故ABFD是矩形,从而AB⊥BF.
又PA⊥底面ABCD,
所以平面PAD⊥平面ABCD,
因为AB⊥AD,故AB⊥平面PAD,
所以AB⊥PD,
在△PDC内,E、F分别是PC、CD的中点,EF∥PD,所以AB⊥EF.
由此得AB⊥平面BEF.
(Ⅱ)因为VC-BEF=1,
所以$\frac{1}{3}×\frac{1}{2}×1×2×\frac{1}{2}PA$=1,
所以PA=6.
点评 本小题主要考查直线与平面的位置关系、三棱锥体积的计算等有关知识,考查空间想象能力和思维能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点与抛物线y2=20x的焦点重合,且其渐近线方程为y=±$\frac{4}{3}$x,则双曲线C的方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{64}$=1 | D. | $\frac{{x}^{2}}{64}$-$\frac{{y}^{2}}{36}$=1 |
3.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程$y=\sqrt{3}x$,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
4.双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$的焦距等于( )
| A. | 2 | B. | 4 | C. | 3 | D. | 6 |
5.某程序框图如图所示,若该程序运行后输出的值是1,则正整数n的值是( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
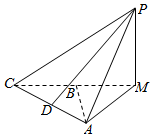 如图,在三棱锥P-AMC中,AC=AM=PM=2,PM⊥面AMC,AM⊥AC,B,D分别为CM,AC的中点.
如图,在三棱锥P-AMC中,AC=AM=PM=2,PM⊥面AMC,AM⊥AC,B,D分别为CM,AC的中点.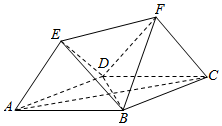 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.