题目内容
已知向量
=(1,2),
=(m,2),且
•
=|
|2,那么m= .
| a |
| b |
| a |
| b |
| a |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积运算性质、模的计算公式即可得出.
解答:
解:∵向量
=(1,2),
=(m,2),且
•
=|
|2,
∴m+4=12+22,
解得m=1.
故答案为:1.
| a |
| b |
| a |
| b |
| a |
∴m+4=12+22,
解得m=1.
故答案为:1.
点评:本题考查了数量积运算性质、模的计算公式,属于基础题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
设a,b是两条不同的直线,α,β是两个不同的平面,a?α,b⊥β,则α∥β是a⊥b的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、即非充分又非必要条件 |
已知一个几何体的三视图如图所示,根据图中尺寸可得该几何体的体积为( )

| A、36π | B、24π |
| C、15π | D、12π |
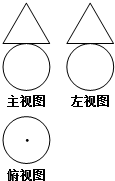 某几何体三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体体积为( )
某几何体三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
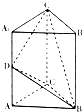 如图,在直三棱柱ABC-A1B1C1中,AC=BC=
如图,在直三棱柱ABC-A1B1C1中,AC=BC=