题目内容
甲、乙两容器中分别盛有两种浓度的某种溶液300mL,从甲容器中取出100mL溶液,将其倒入乙容器中搅匀,再从乙容器中取出100mL溶液,将其倒入甲容器中搅匀,这称为是一次调和,已知第一次调和后,甲、乙两种溶液的浓度分别记为:a1=20%,b1=2%,第n次调和后的甲、乙两种溶液的浓度分别记为:an,bn.
(Ⅰ)请用an,bn分别表示an+1和bn+1;
(Ⅱ)问经过多少次调和后,甲乙两容器中溶液的浓度之差小于0.1%.
(Ⅰ)请用an,bn分别表示an+1和bn+1;
(Ⅱ)问经过多少次调和后,甲乙两容器中溶液的浓度之差小于0.1%.
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(Ⅰ)由题意,第n次调和后的甲、乙两种溶液的浓度分别记为:an,bn,从而可用an,bn分别表示an+1和bn+1;
(Ⅱ)由于题目中的问题是针对浓度之差,所以,我们不妨直接考虑数列{an-bn}.由(I)可得数列{an-bn}是以a1-b1=18%为首项,以
为公比的等比数列,令an-bn<0.1%,即可得出结论.
(Ⅱ)由于题目中的问题是针对浓度之差,所以,我们不妨直接考虑数列{an-bn}.由(I)可得数列{an-bn}是以a1-b1=18%为首项,以
| 1 |
| 2 |
解答:
解:(I)由题意可设在第一次调和后的浓度为a1=20%,b1=2%,bn+1=
=
an+
bn;
an+1=
=
bn+1+
an=
(
an+
bn)+
an=
an+
bn…(6分)
(II)由于题目中的问题是针对浓度之差,所以,我们不妨直接考虑数列{an-bn}.
由(I)可得:an+1-bn+1=(
bn+1+
an)-bn+1=
(an-bn+1)=
[an-(
an+
bn)]=
(an-bn)
=an+1-bn+1=(
bn+1+
an)-bn+1=
(an-bn+1)=
[an-(
an+
bn)]=
(an-bn)…(8分)
所以,数列{an-bn}是以a1-b1=18%为首项,以
为公比的等比数列.
所以,an-bn=18%×(
)n-1…(9分)
由题,令an-bn<0.1%,得(
)n-1<
.
所以,n-1>
=log2180.…(11分)
由27<180<28得7<log2180<8,所以,n>8…(12分)
即第9次调和后两溶液的浓度之差小于0.1%…(13分)
| 100an+300bn |
| (100+300) |
| 1 |
| 4 |
| 3 |
| 4 |
an+1=
| 100bn+1+200an |
| (100+200) |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
(II)由于题目中的问题是针对浓度之差,所以,我们不妨直接考虑数列{an-bn}.
由(I)可得:an+1-bn+1=(
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
=an+1-bn+1=(
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
所以,数列{an-bn}是以a1-b1=18%为首项,以
| 1 |
| 2 |
所以,an-bn=18%×(
| 1 |
| 2 |
由题,令an-bn<0.1%,得(
| 1 |
| 2 |
| 1 |
| 180 |
所以,n-1>
| lg180 |
| lg2 |
由27<180<28得7<log2180<8,所以,n>8…(12分)
即第9次调和后两溶液的浓度之差小于0.1%…(13分)
点评:本题考查数列的性质和应用,考查学生利用数学知识解决实际问题,考查学生的计算能力,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
已知直线l与双曲线C于A,B两点(A,B在同一支上),F1,F2为双曲线的两个焦点,则F1,F2在( )
| A、以A,B为焦点的椭圆上或线段AB的垂直平分线上 |
| B、以A,B为焦点的双曲线上或线段AB的垂直平分线上 |
| C、以AB为直径的圆上或线段AB的垂直平分线上 |
| D、以上说法均不正确 |
某班有50名学生,其中正、副班长各1人,现要选派5人参加一项社区活动,要求正、副班长至少1人参加,问共有多少种选派方法?下面是学生提供的四个计算式,其中错误的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,已知点A(1,
如图,已知点A(1,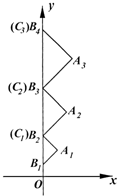 如图,在直角坐标系xOy中,有一组底边长为an的等腰直角三角形AnBnCn(n=1,2,…),底边BnCn依次放置在y轴上(相邻顶点重合),点B1的坐标为(0,b).
如图,在直角坐标系xOy中,有一组底边长为an的等腰直角三角形AnBnCn(n=1,2,…),底边BnCn依次放置在y轴上(相邻顶点重合),点B1的坐标为(0,b).