题目内容
已知直线l与双曲线C于A,B两点(A,B在同一支上),F1,F2为双曲线的两个焦点,则F1,F2在( )
| A、以A,B为焦点的椭圆上或线段AB的垂直平分线上 |
| B、以A,B为焦点的双曲线上或线段AB的垂直平分线上 |
| C、以AB为直径的圆上或线段AB的垂直平分线上 |
| D、以上说法均不正确 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:当直线l垂直于实轴时,F1,F2在AB的垂直平分线上;当直线l不垂直于实轴时,由双曲线定义推导出|AF2|-|BF2|=|AF 1 |-|BF1|<|AB|,由此能求出结果.
解答:
解:当直线l垂直于实轴时,F1,F2在AB的垂直平分线上;
当直线l不垂直于实轴时,设双曲线焦点在x轴,
F1,F2分别为双曲线的左、右焦点,
且A、B都在右支上,由双曲线定义:|AF1|-|AF2|=2a,|BF1|-|BF2|=2a,
则|AF2|-|BF2|=|AF 1 |-|BF1|<|AB|,
由双曲线定义知F1,F2在以A、B为焦点的双曲线上,
故选:B.
当直线l不垂直于实轴时,设双曲线焦点在x轴,
F1,F2分别为双曲线的左、右焦点,
且A、B都在右支上,由双曲线定义:|AF1|-|AF2|=2a,|BF1|-|BF2|=2a,
则|AF2|-|BF2|=|AF 1 |-|BF1|<|AB|,
由双曲线定义知F1,F2在以A、B为焦点的双曲线上,
故选:B.
点评:本题考查双曲线的简单性质的应用,是中档题,解题时要认真审题,注意双曲线定义的合理运用.

练习册系列答案
相关题目
在△ABC中,若3cos2
+5sin2
=4,则tanAtanB=( )
| A-B |
| 2 |
| A+B |
| 2 |
| A、4 | ||
B、
| ||
| C、-4 | ||
D、-
|
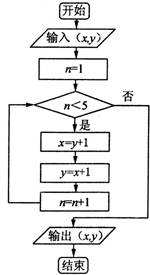
已知某算法的流程图如图所示,若输入x=7,y=6,则输出的有序数对为( )

| A、(13,14) |
| B、(12,13) |
| C、(14,13) |
| D、(13,12) |
若P为△ABC内一点,且
+
+2
=
,在△ABC内随机撒一颗豆子,则此豆子落在△PBC内的概率为( )
| PB |
| PC |
| PA |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|