题目内容
已知曲线C:x2=4y.
(1)若点P是直线y=2x-5上任意一点,过P作C的两条切线PE,PF,切点分别为E,F,M为EF的中点,求证:PM⊥x轴
(2)在(1)的条件下,直线EF是否恒过一定点?若是,求出定点;若不是,说明理由.
(1)若点P是直线y=2x-5上任意一点,过P作C的两条切线PE,PF,切点分别为E,F,M为EF的中点,求证:PM⊥x轴
(2)在(1)的条件下,直线EF是否恒过一定点?若是,求出定点;若不是,说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)对函数求导,设切点坐标,得切线方程.设P(x0,2x0-5)代入两条切线方程,由韦达定理求得M坐标得证;
(2)求出切线PE,PF的方程,可得E,F在直线2x0-5=
x0-y上,即可得出结论.
(2)求出切线PE,PF的方程,可得E,F在直线2x0-5=
| x |
| 2 |
解答:
(1)证明:设M(x,y),E(x1,y1),F(x2,y2),
∵y′=
∴KPE=
,KPF=
,
∴切线PE的方程为y-
=
(x-x1),即y=
x-
….(2分)
同理,切线PF的方程为y=
x-
设P(x0,2x0-5)代入两条切线方程中,
得x1,x2为方程x2-2x0x+8x0-20=0的两个根…(4分)
∴x1+x2=2x0,x=x0,M,P两点的横坐标都是x0
则PM⊥x轴….(6分)
(2)∵y1=
,y2=
,
∴切线PE的方程为y=
x-y1,切线PF的方程为y=
x-y2….(8分)
∴E,F在直线2x0-5=
x0-y上,…(10分)
即(x-4)x0-2y+10=0恒过点(4,5)…(12分)
∵y′=
| x2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴切线PE的方程为y-
| ||
| 4 |
| x1 |
| 2 |
| x1 |
| 2 |
| ||
| 4 |
同理,切线PF的方程为y=
| x2 |
| 2 |
| ||
| 4 |
设P(x0,2x0-5)代入两条切线方程中,
得x1,x2为方程x2-2x0x+8x0-20=0的两个根…(4分)
∴x1+x2=2x0,x=x0,M,P两点的横坐标都是x0
则PM⊥x轴….(6分)
(2)∵y1=
| ||
| 4 |
| ||
| 4 |
∴切线PE的方程为y=
| x1 |
| 2 |
| x2 |
| 2 |
∴E,F在直线2x0-5=
| x |
| 2 |
即(x-4)x0-2y+10=0恒过点(4,5)…(12分)
点评:本题主要考查导数法求切线方程以及直线过定点问题,考查学生分析解决问题的能力,属于中档题..

练习册系列答案
相关题目
在△ABC中,若3cos2
+5sin2
=4,则tanAtanB=( )
| A-B |
| 2 |
| A+B |
| 2 |
| A、4 | ||
B、
| ||
| C、-4 | ||
D、-
|
坐标原点到函数f(x)=ex+1的图象在点(1,f(1))处切线y=g(x)的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,椭圆
如图,椭圆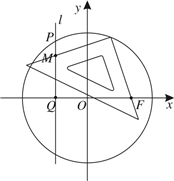 如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且
如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且