题目内容
 如图,已知点A(1,
如图,已知点A(1,| 2 |
| ||
| 2 |
| y2 |
| a2 |
| x2 |
| b2 |
| 2 |
(1)求椭圆C的方程;
(2)求证:直线AB,AD的斜率之和为定值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据点A(1,
)是离心率为
的椭圆C上的一点,建立方程,即可求椭圆C的方程;
(Ⅱ)设直线BD的方程为y=
x+m,代入椭圆方程,设D(x1,y1),B(x2,y2),直线AB、AD的斜率分别为:kAB、kAD,则kAD+kAB=
+
,由此能导出即kAD+kAB=0.
| 2 |
| ||
| 2 |
(Ⅱ)设直线BD的方程为y=
| 2 |
y1-
| ||
| x1-1 |
y2-
| ||
| x2-1 |
解答:
解: (1)由题意,可得e=
(1)由题意,可得e=
=
,
代入A(1,
)得
+
=1,
又a2=b2+c2,…(2分)
解得a=2,b=c=
,
所以椭圆C的方程
+
=1.…(5分)
(2)证明:设直线BD的方程为y=
x+m,
又A、B、D三点不重合,∴m≠0,
设D(x1,y1),B(x2,y2),
则由
得4x2+2
mx+m2-4=0
所以△=-8m2+64>0,
所以-2
<m<2
.
x1+x2=-
m,x1x2=-
…(8分)
设直线AB、AD的斜率分别为:kAB、kAD,
则kAD+kAB=
+
=2
+m•
=2
+m•
=2
-2
=0 (*)
所以kAD+kAB=0,即直线AB,AD的斜率之和为定值.…(12分)
 (1)由题意,可得e=
(1)由题意,可得e=| c |
| a |
| ||
| 2 |
代入A(1,
| 2 |
| 2 |
| a2 |
| 1 |
| b2 |
又a2=b2+c2,…(2分)
解得a=2,b=c=
| 2 |
所以椭圆C的方程
| y2 |
| 4 |
| x2 |
| 2 |
(2)证明:设直线BD的方程为y=
| 2 |
又A、B、D三点不重合,∴m≠0,
设D(x1,y1),B(x2,y2),
则由
|
| 2 |
所以△=-8m2+64>0,
所以-2
| 2 |
| 2 |
x1+x2=-
| ||
| 2 |
| m2-4 |
| 4 |
设直线AB、AD的斜率分别为:kAB、kAD,
则kAD+kAB=
y1-
| ||
| x1-1 |
y2-
| ||
| x2-1 |
| 2 |
| x1+x2-2 |
| x1x2-x1-x2+1 |
=2
| 2 |
-
| ||||||
|
| 2 |
| 2 |
所以kAD+kAB=0,即直线AB,AD的斜率之和为定值.…(12分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若P为△ABC内一点,且
+
+2
=
,在△ABC内随机撒一颗豆子,则此豆子落在△PBC内的概率为( )
| PB |
| PC |
| PA |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
坐标原点到函数f(x)=ex+1的图象在点(1,f(1))处切线y=g(x)的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设z=1-i(i是虚数单位),则复数
的虚部是( )
| 2 |
| z |
| A、1 | B、-1 | C、i | D、-i |
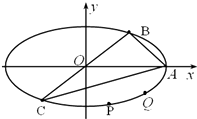 如图,椭圆
如图,椭圆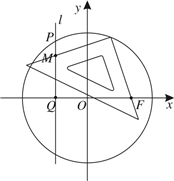 如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且
如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且