题目内容
14．设数列{an}满足a2+a4=10，点Pn（n，an）对任意的n∈N*，都有向量$\overrightarrow{{P_n}{P_{n+1}}}=（1\;，\;3）$，则数列{an}的前n项和Sn=$\frac{3}{2}{n}^{2}$-$\frac{5}{2}$n．分析 点Pn（n，an）对任意的n∈N*，都有向量$\overrightarrow{{P_n}{P_{n+1}}}=（1\;，\;3）$，可得an+1-an=3，数列{an}是公差为3的等差数列，再利用等差数列的通项公式与求和公式即可得出．
解答 解：∵点Pn（n，an）对任意的n∈N*，都有向量$\overrightarrow{{P_n}{P_{n+1}}}=（1\;，\;3）$，∴an+1-an=3，
∴数列{an}是公差为3的等差数列，
∵a2+a4=10，∴2a1+4×3=10，解得a1=-1．
∴Sn=-n+$\frac{n（n-1）}{2}×3$=$\frac{3}{2}{n}^{2}$-$\frac{5}{2}$n．
故答案为：$\frac{3}{2}{n}^{2}$-$\frac{5}{2}$n．
点评 本题考查了等差数列的通项公式与求和公式、向量的坐标运算性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
5．
某制造商为运动会生产一批直径为40mm的乒乓球，现随机抽样检查20只，测得每只球的直径（单位：mm，保留两位小数）如下：
（Ⅰ）完成下面的频率分布表，并画出频率分布直方图；
（Ⅱ）假定乒乓球的直径误差不超过0.02mm为合格品，若这批乒乓球的总数为10 000只，试根据抽样检查结果估计这批产品的合格只数．
某制造商为运动会生产一批直径为40mm的乒乓球，现随机抽样检查20只，测得每只球的直径（单位：mm，保留两位小数）如下：| 40.02 | 40.00 | 39.98 | 40.00 | 39.99 |
| 40.00 | 39.98 | 40.01 | 39.98 | 39.99 |
| 40.00 | 39.99 | 39.95 | 40.01 | 40.02 |
| 39.98 | 40.00 | 39.99 | 40.00 | 39.96 |
| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95，39.97） | 2 | ||
| [39.97，39.99） | 4 | ||
| [39.99，40.01） | 10 | ||
| [40.01，40.03] | 4 | ||
| 合计 |
9．
为了宣传在某市举行的“第十届中国艺术节”，筹委会举办了知识有奖问答活动，随机从15～65岁的市民中抽取n人，回答问题统计结果如图表所示：
（1）求出a，x的值；
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，筹委会决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率．
为了宣传在某市举行的“第十届中国艺术节”，筹委会举办了知识有奖问答活动，随机从15～65岁的市民中抽取n人，回答问题统计结果如图表所示：| 组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
| 第1组 | [15，25） | 5 | 0.5 |
| 第2组 | [25，35） | a | 0.9 |
| 第3组 | [35，45） | 27 | x |
| 第4组 | [45，55） | 9 | 0.36 |
| 第5组 | [55，65） | 3 | 0.2 |
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，筹委会决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率．
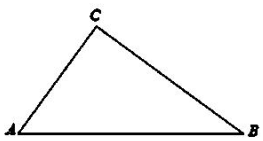如图，A，B，C三地有直道相通，AB=10 千米，AC=6 千米，BC=8千米．现甲、乙两人同时从A地出发匀速前往B地，经过t小时，他们之间的距离为f（t）（单位：千米）．甲的路线是AB，速度为10千米/小时，乙的路线是ACB，速度为16千米/小时．乙到达B地后原地等待．设t=t1时乙到达C地．
已知函数f（x）=x2+2x|x-a|，其中a∈R．