题目内容
4.已知角α的终边上有一点P(1,3),则$\frac{sin(π-α)-sin(\frac{π}{2}+α)}{cos(\frac{3π}{2}-α)+2cos(-π+α)}$的值为-$\frac{2}{5}$.分析 利用三角函数的定义可求得tanα,进而利用诱导公式化简所求即可得解.
解答 解:∵角α的终边上有一点P(1,3),则tanα=3
∴$\frac{sin(π-α)-sin(\frac{π}{2}+α)}{cos(\frac{3π}{2}-α)+2cos(-π+α)}$=$\frac{sinα-cosα}{-sinα-2cosα}$=$\frac{tanα-1}{-tanα-2}$=$\frac{3-1}{-3-2}$=-$\frac{2}{5}$.
故答案为:-$\frac{2}{5}$.
点评 本题主要考查任意角的三角函数的定义,同角三角函数基本关系式的应用,属于基础题.

练习册系列答案
相关题目
15.设P是平行四边形ABCD的对角线的交点,O为任一点,则$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=( )
| A. | $4\overrightarrow{OP}$ | B. | $3\overrightarrow{OP}$ | C. | $2\overrightarrow{OP}$ | D. | $\overrightarrow{OP}$ |
16.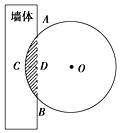 《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
 《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)| A. | 600立方寸 | B. | 610立方寸 | C. | 620立方寸 | D. | 633立方寸 |
 某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.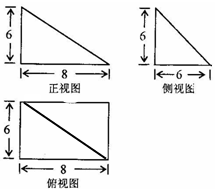 已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示).
已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示).