题目内容
5.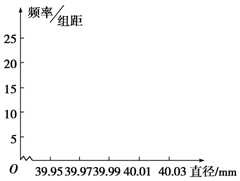 某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:| 40.02 | 40.00 | 39.98 | 40.00 | 39.99 |
| 40.00 | 39.98 | 40.01 | 39.98 | 39.99 |
| 40.00 | 39.99 | 39.95 | 40.01 | 40.02 |
| 39.98 | 40.00 | 39.99 | 40.00 | 39.96 |
| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95,39.97) | 2 | ||
| [39.97,39.99) | 4 | ||
| [39.99,40.01) | 10 | ||
| [40.01,40.03] | 4 | ||
| 合计 |
分析 (I)根据所给的频数和样本容量,计算频率与$\frac{频率}{组距}$,填入表中,画出对应的频率分步直方图;
(II)根据题意求出直径落在[39.97,40.03]范围内的概率,计算对应的合格只数即可.
解答 解:(Ⅰ)根据题意,完成频率分布表如下,
| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95,39.97) | 2 | 0.1 | 5 |
| [39.97,39.99) | 4 | 0.2 | 10 |
| [39.99,40.01) | 10 | 0.5 | 25 |
| [40.01,40.03] | 4 | 0.2 | 10 |
| 合计 | 20 | 1.0 | 50 |

(Ⅱ)误差不超过0.02mm,即直径落在[39.97,40.03]范围内的各个区间的一半概率为
0.1+0.5+0.1=0.7,
这批乒乓球的总数为10000只,根据抽样检查结果估计这批产品的合格只数为
0.7×10000=7000.
点评 本题考查了频率分布表与频率分布直方图的应用问题,也考查了用样本分布估计总体分布的应用问题,是基础题目.

练习册系列答案
相关题目
15.设P是平行四边形ABCD的对角线的交点,O为任一点,则$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=( )
| A. | $4\overrightarrow{OP}$ | B. | $3\overrightarrow{OP}$ | C. | $2\overrightarrow{OP}$ | D. | $\overrightarrow{OP}$ |
16.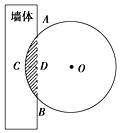 《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
 《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)| A. | 600立方寸 | B. | 610立方寸 | C. | 620立方寸 | D. | 633立方寸 |
20.在△ABC中,角A,B,C所对边分别为a,b,c,若B=30°,b=2,c=2$\sqrt{3}$,则角C=( )
| A. | 60°或120° | B. | 60° | C. | 30°或150° | D. | 30° |
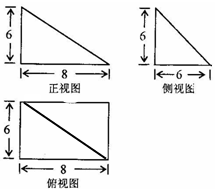 已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示).
已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示).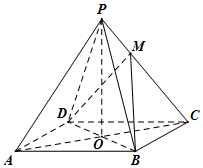 如图,已知四棱锥P-ABCD的底面是菱形,对角线AC,BD交于点O,OA=4,OB=3,OP=4,OP⊥底面ABCD,设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$(λ>0).
如图,已知四棱锥P-ABCD的底面是菱形,对角线AC,BD交于点O,OA=4,OB=3,OP=4,OP⊥底面ABCD,设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$(λ>0).