题目内容
已知f(x)=
(ax-a-x) (a>0且a≠1).
(Ⅰ)判断f(x)的奇偶性;
(Ⅱ)判断f(x)的单调性,并证明你的结论;
(Ⅲ)当x∈[-1,1]时,2f(x)-3b≥0恒成立,求b的取值范围.
| a |
| a2-1 |
(Ⅰ)判断f(x)的奇偶性;
(Ⅱ)判断f(x)的单调性,并证明你的结论;
(Ⅲ)当x∈[-1,1]时,2f(x)-3b≥0恒成立,求b的取值范围.
考点:函数恒成立问题,函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:(Ⅰ)根据函数奇偶性的定义即可判断f(x)的奇偶性;
(Ⅱ)根据函数单调性的定义即可判断f(x)的单调性;
(Ⅲ)根据函数的单调性,将不等式恒成立转化为求函数的最值即可得到结论.
(Ⅱ)根据函数单调性的定义即可判断f(x)的单调性;
(Ⅲ)根据函数的单调性,将不等式恒成立转化为求函数的最值即可得到结论.
解答:
解:( I)函数定义域为R,
∵f(x)=
(ax-a-x) (a>0且a≠1).
∴f(-x)=
(a-x-ax)=-f(x),
∴f(x)为奇函数.
( II)设x1,x2∈R且x1<x2,
∴f(x1)-f(x2)=
[(ax1-a-x1)-(ax2-a-x2)]=
(ax1-ax2+a-x2-a-x1)=
(ax1-ax2+
-
)
=
(ax1-ax2+
)=
(ax1-ax2)(1+
),
当a>1时,
>0,ax1-ax2<0,1+
>0,
∴f(x1)<f(x2)
当0<a<1时,
<0,ax1-ax2>0,1+
>0,
∴f(x1)<f(x2)
∴当a>0,a≠1时,f(x)在定义域内单调递增.
( III)由( II)知,f(x)在R上是增函数,
∴在区间[-1,1]是增函数,
即fmin(x)=f(-1)=
(a-1-a)=-1,
即要使2f(x)-3b≥0恒成立,
b≤f(x),
只需
b≤-1,b≤-
,
∴b的取值范围是(-∞,-
].
∵f(x)=
| a |
| a2-1 |
∴f(-x)=
| a |
| a2-1 |
∴f(x)为奇函数.
( II)设x1,x2∈R且x1<x2,
∴f(x1)-f(x2)=
| a |
| a2-1 |
| a |
| a2-1 |
| a |
| a2-1 |
| 1 |
| ax2 |
| 1 |
| ax1 |
=
| a |
| a2-1 |
| ax1-ax2 |
| ax1+x2 |
| a |
| (a+1)(a-1) |
| 1 |
| ax1+x2 |
当a>1时,
| a |
| (a+1)(a-1) |
| 1 |
| ax1+x2 |
∴f(x1)<f(x2)
当0<a<1时,
| a |
| (a+1)(a-1) |
| 1 |
| ax1+x2 |
∴f(x1)<f(x2)
∴当a>0,a≠1时,f(x)在定义域内单调递增.
( III)由( II)知,f(x)在R上是增函数,
∴在区间[-1,1]是增函数,
即fmin(x)=f(-1)=
| a |
| a2-1 |
即要使2f(x)-3b≥0恒成立,
| 3 |
| 2 |
只需
| 3 |
| 2 |
| 2 |
| 3 |
∴b的取值范围是(-∞,-
| 2 |
| 3 |
点评:本题主要考查函数奇偶性和单调性的应用,根据定义是解决本题的根据,将不等式恒成立转化为求函数的最值是解决本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF.
如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF. 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.
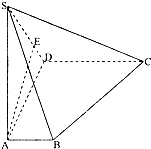 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1.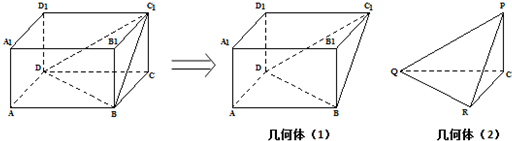
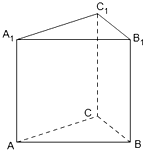 如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.