题目内容
已知数列{an}满足a1=1,an=
(n≥2)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明:
ak>
.
| 4an-1 |
| 2an-1+1 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明:
| n |
 |
| k=1 |
| 3n-2 |
| 2 |
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由{
-
}是以
为首项,以
为公比的等比数列,由此能求出数列{an}的通项公式.
(Ⅱ)由(Ⅰ)知an=
=
-
>
-
,利用放缩法能够证明
ak>
.
| 1 |
| an |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
(Ⅱ)由(Ⅰ)知an=
| 3×4n-1 |
| 2×4n-1+1 |
| 3 |
| 2 |
| 3 |
| 4n+2 |
| 3 |
| 2 |
| 3 |
| 4n |
| n |
 |
| k=1 |
| 3n-2 |
| 2 |
解答:
解:(Ⅰ)∵数列{an}满足a1=1,an=
(n≥2),
∴
=
=
×
+
,
∴
-
=
(
-
),
∵a1-
=
,
∴{
-
}是以
为首项,以
为公比的等比数列,
∴
-
=
(
)n-1,解得an=
,
∵a1=1也适合此式,
∴an=
.
(Ⅱ)∵an=
=
-
=
-
>
-
,
∴
ak=a1+a2+…+an>
n-3×
=
n-1+(
)n>
n-1>
.
∴
ak>
.
| 4an-1 |
| 2an-1+1 |
∴
| 1 |
| an |
| 2an-1+1 |
| 4an-1 |
| 1 |
| 4 |
| 1 |
| an-1 |
| 1 |
| 2 |
∴
| 1 |
| an |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| an-1 |
| 2 |
| 3 |
∵a1-
| 2 |
| 3 |
| 1 |
| 3 |
∴{
| 1 |
| an |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
∴
| 1 |
| an |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 3×4n-1 |
| 2×4n-1+1 |
∵a1=1也适合此式,
∴an=
| 3×4n-1 |
| 2×4n-1+1 |
(Ⅱ)∵an=
| 3×4n-1 |
| 2×4n-1+1 |
| 3 |
| 2 |
| ||
| 2×4n-1+1 |
| 3 |
| 2 |
| 3 |
| 4n+2 |
| 3 |
| 2 |
| 3 |
| 4n |
∴
| n |
 |
| k=1 |
| 3 |
| 2 |
| ||||
1-
|
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 3n-2 |
| 2 |
∴
| n |
 |
| k=1 |
| 3n-2 |
| 2 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,是中档题,解题时要注意递推公式、构造法、放缩法的合理运用.

练习册系列答案
相关题目
若α,β是非零实数,则“α+β=0”是“|α|+|β|>0”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
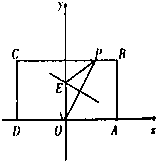 如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足
如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足 如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF.
如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF. 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.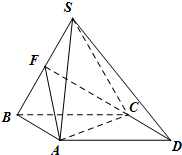 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2