题目内容
15.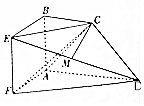 如图,已知四边形ABEF于ABCD分别为正方形和直角梯形,平面ABEF⊥平面ABCD,AB=BC=$\frac{1}{2}$AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.
如图,已知四边形ABEF于ABCD分别为正方形和直角梯形,平面ABEF⊥平面ABCD,AB=BC=$\frac{1}{2}$AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.(1)求证:CM∥平面ABEF;
(2)求三棱锥D-ACF的体积.
分析 (1)几何法:连结AE,BF,交于点O,连结OM,推导出四边形BCMO是平行四边形,由此能证明CM∥平面ABEF.
向量法:以A为原点,AF为x轴,AC为y轴,AB为z轴,建立空间直角坐标系,利用向量法能证明CM∥平面ABEF.
(2)三棱锥D-ACF的体积VD-ACF=VF-ACD,由此能求出结果.
解答 证明:(1)几何法: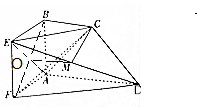 连结AE,BF,交于点O,连结OM,
连结AE,BF,交于点O,连结OM,
∵ABEF是正方形,∴O是AE中点,
∵M是DE中点,∴OM$\underset{∥}{=}$$\frac{1}{2}$AC,
∵ABCD是直角梯形,AB=BC=$\frac{1}{2}$AD=1,
∴BC$\underset{∥}{=}$$\frac{1}{2}$AC,∴BC$\underset{∥}{=}$OM,
∴四边形BCMO是平行四边形,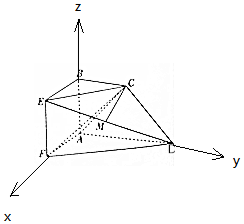
∴BO∥CM,
∵BO?平面ABEF,CM?平面ABEF,
∴CM∥平面ABEF.
(1)向量法:∵四边形ABEF于ABCD分别为正方形和直角梯形,
平面ABEF⊥平面ABCD,AB=BC=$\frac{1}{2}$AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.
∴以A为原点,AF为x轴,AC为y轴,AB为z轴,建立空间直角坐标系,
D(0,2,0),E(1,0,1),M($\frac{1}{2},1,\frac{1}{2}$),C(0,1,1),
$\overrightarrow{CM}$=($\frac{1}{2},0,-\frac{1}{2}$),
平面ABEF的法向量$\overrightarrow{n}$=(0,1,0),
∵$\overrightarrow{n}•\overrightarrow{CM}$=0,CM?平面ABEF,∴CM∥平面ABEF.
解:(2)∵点F到平面ACD的距离AF=1,
S△ACD=S梯形ABCD-S△ABC=$\frac{1}{2}(1+2)×1-\frac{1}{2}×1×1$=1,
∴三棱锥D-ACF的体积:
VD-ACF=VF-ACD=$\frac{1}{3}×AF×{S}_{△ACD}$=$\frac{1}{3}×1×1$=$\frac{1}{3}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,考查推理论能力、运算求解能力、空间思维能力,考查数形结合思想、转化化归思想,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ±$\frac{4}{3}$ | B. | ±$\frac{3}{4}$ | C. | ±$\frac{3}{5}$ | D. | ±$\frac{5}{3}$ |
| A. | 1-2i | B. | 5+4i | C. | 1 | D. | 2 |
| A. | $\frac{17}{18}$ | B. | -$\frac{17}{18}$ | C. | $\frac{18}{19}$ | D. | -$\frac{18}{19}$ |
| 微信群数量(个) | 频数 | 频率 |
| 0~4 | 0.15 | |
| 5~8 | 40 | 0.4 |
| 9~12 | 25 | |
| 13~16 | a | c |
| 16以上 | 5 | b |
| 合计 | 100 | 1 |
(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过12的概率;
(Ⅲ)以(1)中的频率作为概率,若从全市大学生中随机抽取3人,记X表示抽到的是微信群个数超过12的人数,求X的分布列和数学期望E(X).
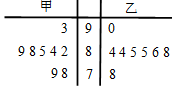 某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )| A. | 甲、乙生产的零件尺寸的中位数相等 | |
| B. | 甲、乙生产的零件质量相当 | |
| C. | 甲生产的零件质量比乙生产的零件质量好 | |
| D. | 乙生产的零件质量比甲生产的零件质量好 |
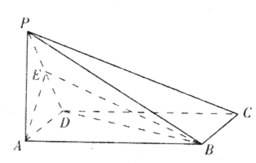 如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD的中点.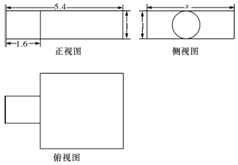 中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器----商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中的x为3.
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器----商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中的x为3.