题目内容

求函数y=2cos2x-
1
2
的图象与x轴及直线x=0、x=π所围成的图形的面积．
考点：二倍角的余弦
专题：计算题,导数的概念及应用
分析：先确定积分区间，再利用定积分表示面积，即可求出结论．
解答： 解：由条件，令y=2cos2x-
1
2
=0，可得x=
π
3
或
2π
3
，
∴图象与x轴交点的横坐标为
π
3
或
2π
3
，
∴S=2
∫
π
3
0
（2cos2x-
1
2
）dx+2
∫
π
2
π
3
（-2cos2x+
1
2
）dx
=2×（
1
2
sin2x-
1
2
x）
|
π
3
0
+2×（-
1
2
sin2x+
1
2
x）
|
π
2
π
3
=
3
+
π
6
．
点评：本题考查利用定积分求面积，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知a∈R，函数f（x）=4x3-2ax+a．
（1）a=1时，求函数的极值；
（2）求f（x）的单调区间．
函数f（x）=6cos2
ωx
2
+
3
sinωx-3（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．
（1）求ω的值及函数f（x）的单调递增区间；
（2）若f（x0）=
8
3
5
，且x0=∈（-
10
3
，
2
3
），求f（x0+1）的值．
设斜率为k1的直线l1与椭圆
x2
2
+y2=1交于不同的A、B两点，直线y=k2x与直线l1的交点为M，（k1≠k2，且k1≠0）．
（Ⅰ）若点M为弦AB的中点，求k1k2的值；
（Ⅱ）把题设中的椭圆一般化为
x2
a2
+
y2
b2
=1（a＞0，b＞0，a≠b），其他条件不变
（i）根据（Ⅰ）的运算结果，写出一个关于k1k2的一般性结论，并判断与证明它的逆命题是否为真命题；
（ii）根据以上探究，在双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）中写出类似结论．
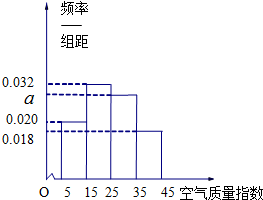去年2月29日，我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀，各类人群可正常活动．惠州市环保局对我市2014年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为（5，15]，（15，25]，（25，35]，（35，45]，由此得到样本的空气质量指数频率分布直方图，如图．
（1）求a的值；
（2）根据样本数据，试估计这一年度的空气质量指数的平均值；（注：设样本数据第i组的频率为pi，第i组区间的中点值为xi（i=1，2，3，…，n），则样本数据的平均值为
.
X
=x1p1+x2p2+x3p3+…+xnpn）
（3）如果空气质量指数不超过15，就认定空气质量为“特优等级”，则从这一年的监测数据中随机抽取3天的数值，其中达到“特优等级”的天数为ξ，求ξ的分布列和数学期望．
已知二次函数y=f（x）的导函数的图象与直线y=2x平行，且y=f（x）在x=-1处取得最小值为0．
（1）求y=f（x）的解析式；
（2）若函数y=f（x）-kx在区间（0，2）有两个不同的零点，求实数k的取值范围．
已知函数f（x）=x2-2ax+2（a+1）lnx，若函数f（x）有两个极值点，求a的取值范围．
已知α∈（-
π
2
，
π
2
），β∈（0，π），求使等式sin（3π-α）=
2
cos（
π
2
-β），
3
cos（-α）=-
2
cos（π+β）同时成立的角α与β．
设函数f（x）=
3
2
cosx+
1
2
sinx+1
（1）求函数f（x）的值域和函数的单调递增区间；
（2）当f（a）=
9
5
，且
π
6
＜α＜
2π
3
时，求sin（2α+
2π
3
）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网