题目内容
已知f(x)为二次函数，且f(－1)＝2，f ′(0)＝0，
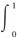f(x)dx＝－2.
(1)求f(x)的解析式；
(2)求f(x)在[－1,1]上的最大值与最小值．
解：(1)设f(x)＝ax2＋bx＋c(a≠0)，
则f ′(x)＝2ax＋b.
由f(－1)＝2，f ′(0)＝0，
得
∴f(x)＝ax2＋(2－a)．
又
f(x)dx＝∫
0[ax2＋(2－a)]dx
＝
＝2－
a＝－2.
∴a＝6，∴c＝－4.从而f(x)＝6x2－4.
(2)∵f(x)＝6x2－4，x∈[－1,1]，
所以当x＝0时，f(x)min＝－4；当x＝±1时，f(x)max＝2.
练习册系列答案
相关题目
x，则f(2 013)＝( )
B.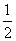
C．2 D．8
则a、b、c的大小关系为( )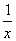
(x>0)图象下方的区域(阴影部分)，从D内随机取一个点M，则点M取自E内的概率为( )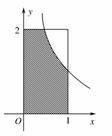
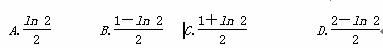
，则a＝________.