题目内容
已知f(x)为偶函数,且f(x+4)=f(-x),当-3≤x≤-2时,f(x)= x,则f(2 013)=( )
x,则f(2 013)=( )
A. B.
B.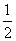 C.2 D.8
C.2 D.8
D

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
题目内容
已知f(x)为偶函数,且f(x+4)=f(-x),当-3≤x≤-2时,f(x)= x,则f(2 013)=( )
x,则f(2 013)=( )
A. B.
B.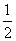 C.2 D.8
C.2 D.8
D

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案