题目内容
已知函数f(x)=ax(a>0,且a≠1)在区间[1,2]上的最大值与最小值的差为 ,则a=________.
,则a=________.
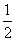 或
或 解析:当0<a<1时,函数f(x)=ax在区间[1,2]上为减函数,
解析:当0<a<1时,函数f(x)=ax在区间[1,2]上为减函数,
最小值为f(2)=a2,最大值为f(1)=a,
依题意,可得a-a2= ,解得a=0(舍去)或a=
,解得a=0(舍去)或a=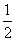 ;
;
当a>1时,函数f(x)=ax在区间[1,2]上为增函数,
最小值为f(1)=a,最大值为f(2)=a2,
依题意,可得a2-a= ,解得a=0(舍去)或a=
,解得a=0(舍去)或a= .
.
综上,a=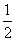 或a=
或a= .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
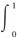 f(x)dx=-2.
f(x)dx=-2. ,g(x)=
,g(x)= ,则函数h(x)=f(x)·g(x)( )
,则函数h(x)=f(x)·g(x)( )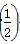 +f(1)+f
+f(1)+f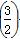 +f(2)+f
+f(2)+f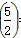 =________.
=________. 的定义域为________.
的定义域为________. 恰有一个零点,则实数a的取值范围是________.
恰有一个零点,则实数a的取值范围是________. ,其中a,b均为非零向量,则|p|的取值范围是( )
,其中a,b均为非零向量,则|p|的取值范围是( ) ] B.[0,1] C.(0,2] D.[0,2]
] B.[0,1] C.(0,2] D.[0,2]