题目内容
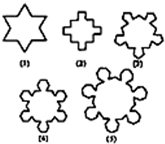 如图,第一个多边形是由正三角形“扩展”而来,第二个多边形是由正四边形“扩展”而来,…,如此类推,设由正n边形“扩展“而来的多边形的边数记为an.则
如图,第一个多边形是由正三角形“扩展”而来,第二个多边形是由正四边形“扩展”而来,…,如此类推,设由正n边形“扩展“而来的多边形的边数记为an.则| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a5 |
| 1 |
| a20 |
考点:归纳推理
专题:推理和证明
分析:观察可得边数与扩展的正n边形的关系为n×(n+1),根据
=
-
求解即可.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:n=3时,边数为3×4=12;
n=4时,边数为4×5=20;
当为n个图形是,边数为n(n+1)
∵
=
-
∴
+
+
+…+
=
+
+…+
=
-
+
-
+…+
-
=
故答案为:
n=4时,边数为4×5=20;
当为n个图形是,边数为n(n+1)
∵
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a5 |
| 1 |
| a20 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 20×21 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 20 |
| 1 |
| 21 |
| 2 |
| 7 |
故答案为:
| 2 |
| 7 |
点评:考查图形的规律性及规律性的应用;得到边数与扩展的正n边形的关系是解决本题的突破点;根据
=
-
求解是本题的难点
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“x=1”是“x2-1=0”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、既非充分也非必要条件 |
| D、充分不必要条件 |
圆
,(θ为参数)的圆心到直线
,(t为参数)的距离是( )
|
|
| A、1 | ||
B、
| ||
C、
| ||
| D、3 |
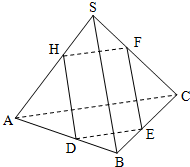 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于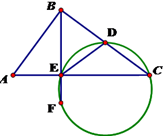 如图,在△ABC中,AB=3,BC=4,CA=5,D是BC的中点,BE⊥AC于E,BE的延长线交△DEC的外接圆于F,则EF的长为
如图,在△ABC中,AB=3,BC=4,CA=5,D是BC的中点,BE⊥AC于E,BE的延长线交△DEC的外接圆于F,则EF的长为