题目内容
12.已知三棱锥P-ABC的所有顶点都在表面积为16π的球O的球面上,AC为球O的直径,当三棱锥P-ABC的体积最大时,设二面角P-AB-C的大小为θ,则sinθ=( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{7}}{3}$ |
分析 AC为球O的直径,当三棱锥P-ABC的体积最大时,△ABC为等腰直角三角形,P在面ABC上的射影为圆心O,过圆心O作OD⊥AB于D,连结PD,则∠PDO为二面角P-AB-C的平面角.
解答 解:如图所示:由已知得球的半径为2,
AC为球O的直径,当三棱锥P-ABC的体积最大时,△ABC为等腰直角三角形,P在面ABC上的射影为圆心O,
过圆心O作OD⊥AB于D,连结PD,则∠PDO为二面角P-AB-C的平面角,
在△ABC△中,PO=2,OD=$\frac{1}{2}$BC=$\sqrt{2}$,∴$PD=\sqrt{6}$,sinθ=$\frac{PO}{PD}=\frac{\sqrt{6}}{3}$.
故选:C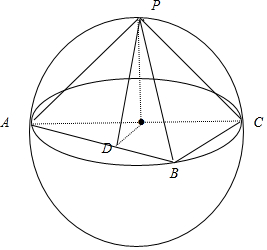
点评 本题考查了与球有关的组合体,关键是要画出图形,找准相应的线线、线面位置关系.属于难题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
2.定义在R上的函数f(x),f′(x)是其导函数,且满足f(x)+f′(x)>2,f(1)=2+$\frac{4}{e}$,则不等式exf(x)>4+2ex的解集为( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,2) | D. | (2,+∞) |
3.某几何体的三视图如图所示,若这个几何体的顶点都在球O的表面上,则球O的表面积是( )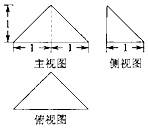

| A. | 2π | B. | 4π | C. | 5π | D. | 20π |
20.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线交于B、C两点,过B作AC的垂线交x轴于点D,若点D到直线BC的距离小于a+$\sqrt{{a}^{2}+{b}^{2}}$,则$\frac{b}{a}$的取值范围为( )
| A. | (0,1) | B. | (1,+∞) | C. | (0,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
7.在(x-$\frac{1}{x}$)10的二项展开式中,x4的系数等于( )
| A. | -120 | B. | -60 | C. | 60 | D. | 120 |
4.已知集合A={x|x2-5x-6≤0},$B=\left\{{\left.x\right|\frac{1}{x-1}>0}\right\}$,则A∩B等于( )
| A. | [-1,6] | B. | (1,6] | C. | [-1,+∞) | D. | [2,3] |