题目内容
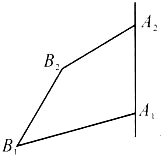 如图,甲船以每小时30
如图,甲船以每小时30| 2 |
| 2 |
考点:解三角形的实际应用
专题:应用题,解三角形
分析:先求出B1B2的距离,再由时间求出乙船航行的速度.
解答:
解:在△A1A2B2中,A1A2=A2B2=10
,∠A1A2B2=60°,∴A1B2=10
在△B1A1B2中,A1B1=20,A1B2=10
,∠B1A1B2=45°,
则由余弦定理得:B1B2=
=10
,v乙=30
.
∴乙船每小时航行30
海里.
故答案为:
| 2 |
| 2 |
在△B1A1B2中,A1B1=20,A1B2=10
| 2 |
则由余弦定理得:B1B2=
400+200-2×20×10
|
| 2 |
| 2 |
∴乙船每小时航行30
| 2 |
故答案为:
点评:本题考查解三角形的实际应用,考查余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=sinxcosx是( )
| A、最小正周期为2π且在[0,π]内有且只有三个零点的函数 |
| B、最小正周期为2π且在[0,π]内有且只有二个零点的函数 |
| C、最小正周期为π且在[0,π]内有且只有三个零点的函数 |
| D、最小正周期为π且在[0,π]内有且只有二个零点的函数 |
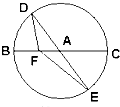 如图,BC是单位圆A的一条直径,F是线段AB上的点,且
如图,BC是单位圆A的一条直径,F是线段AB上的点,且