题目内容
16．设集合A={x∈N|0≤x＜3}的真子集个数为（ ）| A． | 16 | B． | 8 | C． | 7 | D． | 4 |
分析 根据题意，用列举法表示集合A，可得集合A中元素的个数，进而由集合的元素数目与子集数目的关系，计算可得答案．
解答 解：集合A={x|0≤x＜3，x∈Z}={0，1，2}，有3个元素，
则其子集有23-1=7个；
故选C．
点评 本题考查集合的元素数目与子集数目的关系，若集合中有n个元素，则其有2n个子集，有2n-1个真子集．
练习册系列答案
阅读快车系列答案
相关题目
4．
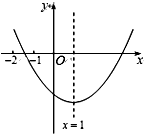已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列结论中：
①b2-4ac＞0；
②abc＞0；
③b=-2a；
④9a+3b+c＜0，
正确结论的个数是（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列结论中：①b2-4ac＞0；
②abc＞0；
③b=-2a；
④9a+3b+c＜0，
正确结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如表资料：
（1）请根据12月2日至12月4日的数据，求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$（其中已计算出$\widehat{b}$=$\frac{5}{2}$）；
（2）若由线性回归方程得到的估计数据与所选出的检验数据（选取的检验数据是12月1日与12月5日
的两组数据）的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？
| 日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x（°C） | 10 | 11 | 13 | 12 | 8 |
| 发芽数y（颗） | 23 | 25 | 30 | 26 | 16 |
（2）若由线性回归方程得到的估计数据与所选出的检验数据（选取的检验数据是12月1日与12月5日
的两组数据）的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？
1．为了得到函数y=sin2x-cos2x的图象，可以将函数y=$\sqrt{2}$cos2x的图象（ ）
| A． | 向左平行移动$\frac{3π}{8}$个单位 | B． | 向右平行移动$\frac{3π}{8}$个单位 | ||
| C． | 向左平行移动$\frac{3π}{4}$个单位 | D． | 向右平行移动$\frac{3π}{4}$个单位 |
8．已知|$\overrightarrow a$|=4cos$\frac{π}{8}$，|$\overrightarrow b$|=2sin$\frac{π}{8}$，$\overrightarrow a$•$\overrightarrow b$=-$\sqrt{2}$，则$\overrightarrow a$与$\overrightarrow b$的夹角为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{4}$ | C． | $\frac{3π}{4}$ | D． | $\frac{2π}{3}$ |
5．已知双曲线C：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的渐近线方程为y=±$\frac{3}{4}$x，且其右焦点为（5，0），则双曲线C的方程为（ ）
| A． | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B． | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | C． | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D． | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
6．
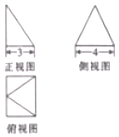某几何体的三视图如图所示，其侧视图是一个等边三角形，则此几何体的体积是（ ）
某几何体的三视图如图所示，其侧视图是一个等边三角形，则此几何体的体积是（ ）| A． | 24$\sqrt{3}$ | B． | 8$\sqrt{3}$ | C． | 16$\sqrt{3}$ | D． | 16 |