题目内容

17．已知函数f（x）=$\left\{\begin{array}{l}{log_2}（1-x），x＜1\\-{（x-2）^2}+2，x≥1\end{array}$，则关于x的方程f（|x|）=a（a∈R）的实根个数不可能为（　　）
A．5个B．4个C．3个D．2个

分析 由题意可得求函数y=f（|x|）的图象和直线y=a的交点个数．作出函数y=f（|x|）的图象，平移直线y=a，即可得到所求交点个数，进而得到结论

解答 解：函数f（x）=$\left\{\begin{array}{l}{log_2}（1-x），x＜1\\-{（x-2）^2}+2，x≥1\end{array}$，方程f（|x|）=a，（a∈R）实根个数，
即为函数y=f（|x|）和直线y=a的交点个数．
由y=f（|x|）为偶函数，可得图象关于y轴对称．
作出函数y=f（|x|）的图象，如图，
平移直线y=a，可得它们有2个、3个、4个交点．
不可能有5个交点，即不可能有5个实根，
故选：A．

点评 本题考查方程的实根个数问题的解法，注意运用转化思想和数形结合的方法，考查判断和作图能力，属于中档题．

练习册系列答案
相关题目
7．若正三棱柱的所有棱长均为a，且其体积为16$\sqrt{3}$，则a=4．
8．已知|$\overrightarrow a$|=4cos$\frac{π}{8}$，|$\overrightarrow b$|=2sin$\frac{π}{8}$，$\overrightarrow a$•$\overrightarrow b$=-$\sqrt{2}$，则$\overrightarrow a$与$\overrightarrow b$的夹角为（　　）
A．$\frac{π}{3}$B．$\frac{π}{4}$C．$\frac{3π}{4}$D．$\frac{2π}{3}$
5．已知双曲线C：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的渐近线方程为y=±$\frac{3}{4}$x，且其右焦点为（5，0），则双曲线C的方程为（　　）
A．$\frac{x^2}{9}-\frac{y^2}{16}=1$B．$\frac{x^2}{16}-\frac{y^2}{9}=1$C．$\frac{x^2}{3}-\frac{y^2}{4}=1$D．$\frac{x^2}{4}-\frac{y^2}{3}=1$
12．执行如图所示程序框图所表示的算法，输出的结果是80，则判断框中应填入（　　）
A．n≤8B．n≥8C．n≤9D．n≥9
2．已知函数f（x）为奇函数，且当x＞0时，f（x）=x2-2x+3，则f（x）的解析式是f（x）=$\left\{\begin{array}{l}{-{x}^{2}-2x-3，（x＜0）}\\{0，（x=0）}\\{{x}^{2}-2x+3，（x＞0）}\end{array}\right.$．
9．设a=log0.32，b=ln2，c=5${\;}^{\frac{1}{2}}}$，则（　　）
A．a＜b＜cB．b＜c＜aC．c＜a＜bD．c＜b＜a
6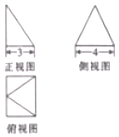．某几何体的三视图如图所示，其侧视图是一个等边三角形，则此几何体的体积是（　　）
A．24$\sqrt{3}$B．8$\sqrt{3}$C．16$\sqrt{3}$D．16
7．当圆锥的侧面积和底面积的比值是2时，圆锥轴截面的顶角等于（　　）
A．45°B．60°C．90°D．120°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网