题目内容
16.已知函数f(x)定义域为R,若存在常数f(x),使$|f(x)|≤\frac{k}{2017}|x|$对所有实数都成立,则称函数f(x)为“期望函数”,给出下列函数:①f(x)=x2②f(x)=xex③$f(x)=\frac{x}{{{x^2}-x+1}}$④$f(x)=\frac{x}{{{e^x}+1}}$
其中函数f(x)为“期望函数”的是③④.(写出所有正确选项的序号)
分析 ①:假设函数f(x)为“期望函数“,则|f(x)|=x2≤$\frac{k}{2017}$|x|,当x=0时,k∈R,x≠0时,化为k≥2017|x|,因此不存在k>0,使得x≠0成立,因此假设不正确,
②:同理①可判定;
对于③:假设函数f(x)为“期望函数“,则则|f(x)|=$\frac{|x|}{{x}^{2}-x+1}≤\frac{k}{2017}|x|$,当x=0时,k∈R,x≠0时,化为k≥2017×$\frac{1}{{x}^{2}-x+1}$=$\frac{2017}{(x-\frac{1}{2})^{2}+\frac{3}{4}}$,k≥$\frac{8064}{3}$.存在常数k>0,使$|f(x)|≤\frac{k}{2017}|x|$对所有实数都成立;
对于④,同理③可判定;
解答 解:对于①:假设函数f(x)为“期望函数“,则|f(x)|=x2≤$\frac{k}{2017}$|x|,
当x=0时,k∈R,x≠0时,化为k≥2017|x|,因此不存在k>0,使得x≠0成立,因此假设不正确,即函数f(x)不是“期望函数”;
对于②:同理①可得②也不是“期望函数”;
对于③:假设函数f(x)为“期望函数“,则则|f(x)|=$\frac{|x|}{{x}^{2}-x+1}≤\frac{k}{2017}|x|$,
当x=0时,k∈R,x≠0时,化为k≥2017×$\frac{1}{{x}^{2}-x+1}$=$\frac{2017}{(x-\frac{1}{2})^{2}+\frac{3}{4}}$,∴k≥$\frac{8064}{3}$.∴存在常数k>0,使$|f(x)|≤\frac{k}{2017}|x|$对所有实数都成立,∴③是“期望函数”;
对于④,假设函数f(x)为“期望函数“,则|f(x)|=$\frac{|x|}{{e}^{x}+1}≤\frac{k}{2017}|x|$,
当x=0时,k∈R,x≠0时,化为k≥2017×$\frac{1}{{e}^{x}+1}$,k≥2017,.∴存在常数k>0,使$|f(x)|≤\frac{k}{2017}|x|$对所有实数都成立,∴④是“期望函数”;
故答案为:③④.
点评 本题考查了新定义函数、分类讨论方法、函数的单调性及其最值,考查了推理能力与计算能力,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
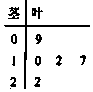 如图是一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的平均数、中位数分别为( )
如图是一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的平均数、中位数分别为( )| A. | 14,12 | B. | 12,14 | C. | 14,10 | D. | 10,12 |
| 价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
| 日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程$y=bx+\hat a$,其中$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{(x_i^{\;}-\overline x)}^2}}}},\hat a=\overline y-\hat b\overline x$.
| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
 如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=2,AC⊥CD,且平面PCD⊥平面ABCD.
如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=2,AC⊥CD,且平面PCD⊥平面ABCD.