题目内容
如图，已知A、B、C、D四点共圆，延长AD和BC相交于点E，AB＝AC.
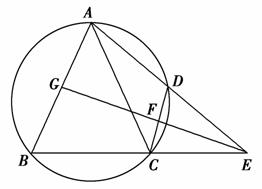
(1)证明：AB2＝AD·AE；
(2)若EG平分∠AEB，且与AB、CD分别相交于点G、F，证明：∠CFG＝∠BGF.
(1)如图，连接BD.
因为AB＝AC，所以∠ABC＝∠ACB＝∠ADB.
又因为∠BAD＝∠EAB，所以△ABD
△AEB，
所以
＝
，即AB2＝AD·AE.
(2)因为A、B、C、D四点共圆，所以∠ABC＝∠EDF.
又因为∠DEF＝∠BEG，所以∠DFE＝∠BGF.
又因为∠DFE＝∠CFG，所以∠CFG＝∠BGF.
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
，AB是圆O的直径，C为圆O上一点，且BC＝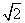
，过点B的圆O的切线交AC延长线于点D，则DA＝________.
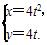(t为参数)上，则|PF|＝( )
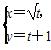(t为参数)，曲线C2的极坐标方程为ρsinθ－ρcosθ＝3，则C1与C2的交点在直角坐标系中的坐标为________．
<
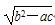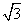a”“索”的“因”应是( )