题目内容
已知函数f(x)=sinx+ex+x2010,令f1(x)=f ′(x),f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),则f2014(x)=( )
A.sinx+ex B.cosx+ex
C.-sinx+ex D.-cosx+ex
C
[解析] f1(x)=f ′(x)=cosx+ex+2010x2009,
f2(x)=f1′(x)=-sinx+ex+2010×2009x2008,
f3(x)=f2′(x)=-cosx+ex+2010×2009×2008x2007,
f4(x)=f3′(x)=sinx+ex+2010×2009×2008×2007x2006,
由此可以看出,该函数前2项的和成周期性变化,周期T=4;
而f2014(x)=f ′2013(x),此时其最后一项的导数已变为0.
故求f2014(x)的值,只需研究该函数前2项和的变化规律即可,于是,f2014(x)=f(2+4×503)(x)=-sinx+ex.

练习册系列答案
相关题目
 ,则n与p的值分别为( )
,则n与p的值分别为( ) B.20与
B.20与
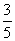
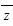 是复数z的共轭复数,若z·
是复数z的共轭复数,若z· ,
, },i是虚数单位,Z为整数集,则集合Z∩M中的元素个数是( )
},i是虚数单位,Z为整数集,则集合Z∩M中的元素个数是( ) <
<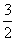 ,
, <
< ,
, <
< ,
,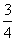 ,则a1的取值范围是( )
,则a1的取值范围是( ) +
+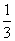 -
-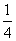 +…+
+…+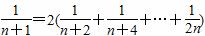 时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证n=( )时等式成立.( )
时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证n=( )时等式成立.( )