题目内容
1.如图,在正方体ABCD-A1B1C1D1中,B1D与C1D1所成角的余弦值是( )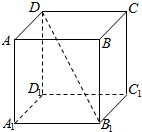
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
分析 由C1D1∥A1B1,得∠A1B1D是B1D与C1D1所成角,由此能求出B1D与C1D1所成角的余弦值.
解答 解:∵C1D1∥A1B1,∴∠A1B1D是B1D与C1D1所成角,
设正方体ABCD-A1B1C1D1中棱长为a,
∴${A}_{1}D=\sqrt{2}a$,B1D=$\sqrt{3}a$,
∴cos∠A1B1D=$\frac{{A}_{1}{B}_{1}}{{B}_{1}D}$=$\frac{a}{\sqrt{3}a}$=$\frac{\sqrt{3}}{3}$.
∴B1D与C1D1所成角的余弦值是$\frac{\sqrt{3}}{3}$.
故选:B.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
9.直线y=-$\sqrt{3}$x+1的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
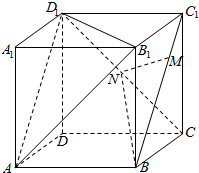 如图,正方体ABCD-A1B1C1D1中,N为CD1中点,M为线段BC1上的动点(M不与B,C1重合),以下四个命题:
如图,正方体ABCD-A1B1C1D1中,N为CD1中点,M为线段BC1上的动点(M不与B,C1重合),以下四个命题: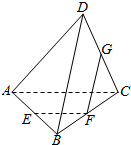 如图,在空间四边形ABCD中,E,F,G分别是AB,BC,CD的中点,
如图,在空间四边形ABCD中,E,F,G分别是AB,BC,CD的中点, 空间四边形ABCD中,E、F分别是AB、CD的中点,AD⊥BC,且AD=4,BC=6,求异面直线EF与BC所成角的大小.
空间四边形ABCD中,E、F分别是AB、CD的中点,AD⊥BC,且AD=4,BC=6,求异面直线EF与BC所成角的大小.