题目内容
6.已知f(x)在R上是以3为周期的偶函数,f(-2)=3,若tanα=2,则f(10sin2α)的值是( )| A. | 1 | B. | -1 | C. | 3 | D. | 8 |
分析 根据三角函数的倍角公式求出三角函数值,利用函数奇偶性和周期性的关系将条件进行转化即可.
解答 解:∵tanα=2,
∴sin2α=2sinαcosα=$\frac{2sinαcosα}{sin^2α+cos^2α}$=$\frac{2tanα}{1+ta{n}^{2}α}$=$\frac{2×2}{1+{2}^{2}}$=$\frac{4}{5}$,
则10sin2α=10×$\frac{4}{5}$=8,
∵f(x)在R上是以3为周期的偶函数,
∴f(10sin2α)=f(8)=f(8-6)=f(2),
∵f(-2)=3,
∴f(2)=3,
即f(10sin2α)=f(2)=3,
故选:C.
点评 本题主要考查函数值的计算,根据三角函数的倍角公式以及函数的奇偶性和周期性的关系将条件进行转化求解即可.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
1.如图,在正方体ABCD-A1B1C1D1中,B1D与C1D1所成角的余弦值是( )
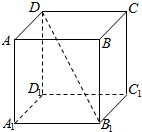

| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
11.若直线x+my-2=0的倾斜角为30°,则实数m的值是( )
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
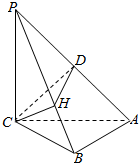 在三棱锥P-ABC中,PC⊥平面ABC,△PAC是等腰直角三角形,PA=6,AB⊥BC,CH⊥PB,垂足为H,D为PA的中点,则当△CDH的面积最大时,CB=$\sqrt{6}$.
在三棱锥P-ABC中,PC⊥平面ABC,△PAC是等腰直角三角形,PA=6,AB⊥BC,CH⊥PB,垂足为H,D为PA的中点,则当△CDH的面积最大时,CB=$\sqrt{6}$.