设直线l是过圆(x-4)2+y2=25与x轴正半轴交点的切线.试求到l与到此圆心的距离之比为3:2的点的轨迹.并指出此轨迹的顶点坐标.焦点坐标和离心率．题目和参考答案——青夏教育精英家教网——

题目内容

10．设直线l是过圆（x-4）²+y²=25与x轴正半轴交点的切线，试求到l与到此圆心的距离之比为3：2的点的轨迹，并指出此轨迹的顶点坐标、焦点坐标和离心率．

分析求出直线l，利用点到l与到此圆心的距离之比为3：2，建立方程，即可得出结论．

解答解：圆（x-4）²+y²=25与x轴正半轴交点坐标为（9，0），∴直线l：x=9．
设点的坐标为（x，y），则4|x-9|²=9（x-4）²+y²，
化简得$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{180}$=1，
∴a=6$\sqrt{5}$，b=6，c=2$\sqrt{39}$，
∴顶点坐标（0，±6$\sqrt{5}$），（±6，0）、焦点坐标（0，±2$\sqrt{39}$），离心率e=$\frac{c}{a}$=$\frac{\sqrt{195}}{15}$．

点评本题考查轨迹方程，考查椭圆的性质，确定轨迹方程是关键．

练习册系列答案

优翼阅读给力系列答案

领航中考命题调研系列答案

初中古诗文详解系列答案

口算应用题卡系列答案

中考考点经典新题系列答案

英语阅读系列答案

课堂导学案系列答案

中考新航标初中重点知识总复习指导系列答案

金点新课标同步精练系列答案

教材精析精练字词句篇系列答案

相关题目

20．函数f（x）=$\sqrt{x-1}$+lg（6-2x）的定义域是（　　）

1．如图，在正方体ABCD-A₁B₁C₁D₁中，B₁D与C₁D₁所成角的余弦值是（　　）

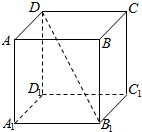
$\frac{{\sqrt{2}}}{2}$

$\frac{{\sqrt{3}}}{3}$

$\frac{{\sqrt{3}}}{2}$

$\frac{{\sqrt{6}}}{3}$

18．设函数f（x）=e^x-ax²-2x-1．
（1）若曲线y=f（x）在点（1，f（1））处的切线为l，且l在y轴上的截距为-2，求实数a的值；
（2）若1＜a＜2，证明：存在x₀∈（-$\frac{1}{a}$，-$\frac{1}{4}$），使得f′（x₀）=0，且f（x₀）＜$\frac{15}{16}$．

5．下列命题正确的个数是（　　）
①a•c=b²是a，b，c成等比数列的必要条件．
②公比q＞1的等比数列的各项均大于1．
③常数列是公比为1的等比数列．
④{lg2ⁿ}}是等差数列而不是等比数列．

15．定点A到定直线1的距离为a，过点A任意作射线交直线l于点Q．
（1）在射线AQ上取一点到P，使得|AP|=$\frac{1}{2}$|AQ|，求点P的轨迹方程；
（2）延长AQ到P′，使得|AP′|=b，求点P′的轨迹方程．

2．已知函数y=f（x）是定义在R上的增函数，且满足f（x-2）+f（-x+2）=0，若任意的x，y∈R，不等式f（x²-4x+4）+f（y²-6y）≤0恒成立，则当x≥2时，x²+y²的取值范围（　　）

[2，2+$\sqrt{13}$]

[4，22+6$\sqrt{13}$]

19．已知函数f（x）=a^x-a•x，e=2.71828…为自然对数的底数．
（Ⅰ）当a=e时，求函数f（x）的单调区间；
（Ⅱ）设a≥e且n∈N^*，比较$\frac{n（n+1）}{2}$与$\frac{ln（a-1）+ln（2a-1）+ln（3a-1）+…+ln（na-1）}{lna}$的大小，并加以证明．

20．用二分法求方程x²=（$\frac{1}{2}$）^x-2的近似解时，所取的初始区间可以是（　　）