题目内容
(本小题满分12分)
设函数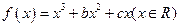 ,已
,已 知
知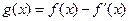
是奇函数.
(Ⅰ)求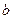 、
、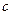 的值;
的值;
(Ⅱ)求 的单调区间与极值.
的单调区间与极值.
设函数
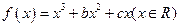 ,已
,已 知
知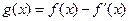
是奇函数.
(Ⅰ)求
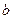 、
、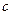 的值;
的值; (Ⅱ)求
 的单调区间与极值.
的单调区间与极值.(Ⅰ) ,
,
(Ⅱ) 和
和 是函数
是函数 是单调递增区间,
是单调递增区间,
 是函数
是函数 是单调递减区间。
是单调递减区间。
 在
在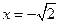 时,取得极大值,极大值为
时,取得极大值,极大值为 ;
;
 在
在 时,取得极小值,极小值为
时,取得极小值,极小值为
 ,
,
(Ⅱ)
 和
和 是函数
是函数 是单调递增区间,
是单调递增区间, 是函数
是函数 是单调递减区间。
是单调递减区间。 在
在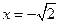 时,取得极大值,极大值为
时,取得极大值,极大值为 ;
; 在
在 时,取得极小值,极小值为
时,取得极小值,极小值为
解:(Ⅰ)∵ ,∴
,∴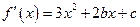 .
.
从而 =
=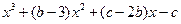
∵
 是一个R上的奇函数,所以
是一个R上的奇函数,所以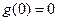 得
得 ,由奇函数定义得
,由奇函数定义得 ;
;
(Ⅱ)由(Ⅰ)知 ,从而
,从而 ,由此可知,
,由此可知,

 和
和 是函数
是函数 是单调递增区间;
是单调递增区间;

 是函数
是函数 是单调递减区间;
是单调递减区间;
∴ 在
在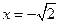 时,取得极大值,极大值为
时,取得极大值,极大值为 ;
;
 在
在 时,取得极小值,极小值为
时,取得极小值,极小值为 .
.
 ,∴
,∴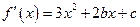 .
.从而
 =
=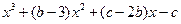
∵

 是一个R上的奇函数,所以
是一个R上的奇函数,所以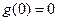 得
得 ,由奇函数定义得
,由奇函数定义得 ;
;(Ⅱ)由(Ⅰ)知
 ,从而
,从而 ,由此可知,
,由此可知,

 和
和 是函数
是函数 是单调递增区间;
是单调递增区间;
 是函数
是函数 是单调递减区间;
是单调递减区间;∴
 在
在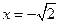 时,取得极大值,极大值为
时,取得极大值,极大值为 ;
; 在
在 时,取得极小值,极小值为
时,取得极小值,极小值为 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
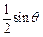 x2-2x+c,过点
x2-2x+c,过点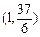 ,且在(-2,1)内单调递减,在[1,
,且在(-2,1)内单调递减,在[1,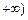 上单调递增。
上单调递增。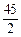 恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。
恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。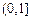 ,an+1=f(an),求证:an+1>8·lnan(n∈N*)。
,an+1=f(an),求证:an+1>8·lnan(n∈N*)。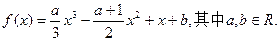
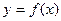 在点
在点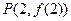 处的切线方程为
处的切线方程为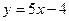 ,求函数
,求函数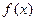 的解析式;
的解析式;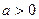 时,讨论函数
时,讨论函数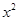 +
+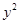 =1,那么(1-xy)(1+xy)有( )
=1,那么(1-xy)(1+xy)有( )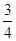 和最大值1
和最大值1 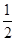 和最大值1
和最大值1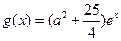 ,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。
,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。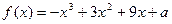 ,若
,若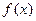 在区间[-2,2]上的最大值为20.
在区间[-2,2]上的最大值为20.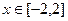 时,
时,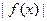 ≤m,(m>0)恒成立.求m的取值范围.
≤m,(m>0)恒成立.求m的取值范围.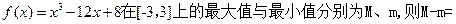 ____.
____.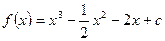 ,若对任意
,若对任意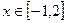 都有
都有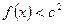 ,则
,则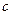 的取值范围是 .
的取值范围是 .