题目内容
(本小题12分)已知函数f(x)=ax3+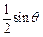 x2-2x+c,过点
x2-2x+c,过点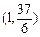 ,且在(-2,1)内单调递减,在[1,
,且在(-2,1)内单调递减,在[1,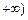 上单调递增。
上单调递增。
(1)证明sinθ=1,并求f(x)的解析式。
(2)若对于任意的x1,x2∈[m,m+3](m≥0),不等式|f(x1)-f(x2)|≤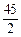 恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。
恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。
(3)已知数列{an}中,a1∈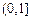 ,an+1=f(an),求证:an+1>8·lnan(n∈N*)。
,an+1=f(an),求证:an+1>8·lnan(n∈N*)。
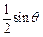 x2-2x+c,过点
x2-2x+c,过点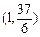 ,且在(-2,1)内单调递减,在[1,
,且在(-2,1)内单调递减,在[1,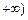 上单调递增。
上单调递增。(1)证明sinθ=1,并求f(x)的解析式。
(2)若对于任意的x1,x2∈[m,m+3](m≥0),不等式|f(x1)-f(x2)|≤
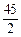 恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。
恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。(3)已知数列{an}中,a1∈
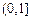 ,an+1=f(an),求证:an+1>8·lnan(n∈N*)。
,an+1=f(an),求证:an+1>8·lnan(n∈N*)。(1)f(x)= 即为所求,(2)存在m且m∈[0,1]合乎题意(3)同解析。
即为所求,(2)存在m且m∈[0,1]合乎题意(3)同解析。
 即为所求,(2)存在m且m∈[0,1]合乎题意(3)同解析。
即为所求,(2)存在m且m∈[0,1]合乎题意(3)同解析。解:(1)∵ (x)=3ax2+sinθx-2
(x)=3ax2+sinθx-2
由题设可知: 即
即
 ∴sinθ=1。(2分)
∴sinθ=1。(2分)
从而a= ,∴f(x)=
,∴f(x)= ,而又由f(1)=
,而又由f(1)= 得,c=
得,c=
∴f(x)= 即为所求。 (4分)
即为所求。 (4分)
(2) (x)=x2+x-2=(x+2)(x-1)易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数。
(x)=x2+x-2=(x+2)(x-1)易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数。
(i)当m>1时,f(x)在[m,m+3]上递增。故f(x)max=f(m+3),f(x)min=f(m)
由f(m+3)-f(m)= (m+3)3+
(m+3)3+ (m+3)2-2(m+3)-
(m+3)2-2(m+3)- =3m2+12m+
=3m2+12m+ 得-5≤m≤1。这与条件矛盾故舍。 (6分)
得-5≤m≤1。这与条件矛盾故舍。 (6分)
(ii)当0≤m≤1时,f(x)在[m,1]上递减,在[1,m+3]上递增。
∴f(x)min=f(1),f(x)max={f(m),f(m+3)}max
又f(m+3)-f(m)=3m2+12m+ =3(m+2)2-
=3(m+2)2- >0(0≤m≤1),∴f(x)max=f(m+3)
>0(0≤m≤1),∴f(x)max=f(m+3)
∴|f(x1)-f(x2)| ≤f(x)max-f(x)min="f(m+3)-f(1)" ≤f(4)-f(1)=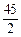 恒成立
恒成立
故当0≤m≤1原式恒成立。 (8分)
综上:存在m且m∈[0,1]合乎题意。 (9分)
(3)∵a1∈(0,1 ,∴a2∈
,∴a2∈ ,故a2>2
,故a2>2
假设n=k(k≥2,k∈N*)时,ak>2。则ak+1=f(ak)>f(2)=8>2
故对于一切n(n≥2,n∈N*)均有an>2成立。 (11分)
令g(x)=
得 =
=
当x∈(0,2)时 (x)<0,x∈(2,+∞)时,
(x)<0,x∈(2,+∞)时, (x)>0,
(x)>0,
∴g(x)在x∈[2,+∞ 时为增函数。
时为增函数。
而g(2)=8-8ln2>0,即当x∈[2,+∞ 时,g(x)≥g(2)>0恒成立。
时,g(x)≥g(2)>0恒成立。
∴g(an)>0,(n≥2)也恒成立。即:an+1>8lnan(n≥2)恒成立。
而当n=1时,a2=8,而8lna1≤0,∴a2>8lna1显然成立。
综上:对一切n∈N*均有an+1>8lnan成立。
 (x)=3ax2+sinθx-2
(x)=3ax2+sinθx-2由题设可知:
 即
即
 ∴sinθ=1。(2分)
∴sinθ=1。(2分)从而a=
 ,∴f(x)=
,∴f(x)= ,而又由f(1)=
,而又由f(1)= 得,c=
得,c=
∴f(x)=
 即为所求。 (4分)
即为所求。 (4分)(2)
 (x)=x2+x-2=(x+2)(x-1)易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数。
(x)=x2+x-2=(x+2)(x-1)易知f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数。(i)当m>1时,f(x)在[m,m+3]上递增。故f(x)max=f(m+3),f(x)min=f(m)
由f(m+3)-f(m)=
 (m+3)3+
(m+3)3+ (m+3)2-2(m+3)-
(m+3)2-2(m+3)- =3m2+12m+
=3m2+12m+ 得-5≤m≤1。这与条件矛盾故舍。 (6分)
得-5≤m≤1。这与条件矛盾故舍。 (6分)(ii)当0≤m≤1时,f(x)在[m,1]上递减,在[1,m+3]上递增。
∴f(x)min=f(1),f(x)max={f(m),f(m+3)}max
又f(m+3)-f(m)=3m2+12m+
 =3(m+2)2-
=3(m+2)2- >0(0≤m≤1),∴f(x)max=f(m+3)
>0(0≤m≤1),∴f(x)max=f(m+3)∴|f(x1)-f(x2)| ≤f(x)max-f(x)min="f(m+3)-f(1)" ≤f(4)-f(1)=
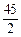 恒成立
恒成立故当0≤m≤1原式恒成立。 (8分)
综上:存在m且m∈[0,1]合乎题意。 (9分)
(3)∵a1∈(0,1
 ,∴a2∈
,∴a2∈ ,故a2>2
,故a2>2假设n=k(k≥2,k∈N*)时,ak>2。则ak+1=f(ak)>f(2)=8>2
故对于一切n(n≥2,n∈N*)均有an>2成立。 (11分)
令g(x)=

得
 =
=
当x∈(0,2)时
 (x)<0,x∈(2,+∞)时,
(x)<0,x∈(2,+∞)时, (x)>0,
(x)>0,∴g(x)在x∈[2,+∞
 时为增函数。
时为增函数。而g(2)=8-8ln2>0,即当x∈[2,+∞
 时,g(x)≥g(2)>0恒成立。
时,g(x)≥g(2)>0恒成立。∴g(an)>0,(n≥2)也恒成立。即:an+1>8lnan(n≥2)恒成立。
而当n=1时,a2=8,而8lna1≤0,∴a2>8lna1显然成立。
综上:对一切n∈N*均有an+1>8lnan成立。

练习册系列答案
相关题目
 , (1)若
, (1)若 在
在 处有极值,求a;
处有极值,求a; 上为增函数,求a的取值范围.
上为增函数,求a的取值范围.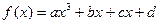 的图象与y轴的交点为点P,且曲线在点P处的切线方程为
的图象与y轴的交点为点P,且曲线在点P处的切线方程为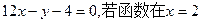 处取得极值0,试求函数的单调区间。
处取得极值0,试求函数的单调区间。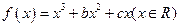 ,已
,已 知
知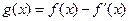
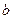 、
、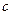 的值;
的值;  的单调区间与极值.
的单调区间与极值. 在
在 上有最小值,实数
上有最小值,实数 的取值范围为________;
的取值范围为________; 在区间
在区间 上最大值与最小值分别是 ( )
上最大值与最小值分别是 ( ) 函数
函数 在
在 处有极小值
处有极小值 ,则
,则 .
. 的极大值为 ( )
的极大值为 ( )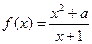 在
在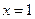 处取得极值,则实数
处取得极值,则实数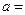 ▲ .
▲ .