题目内容
下列四个命题中正确命题的个数是( )
(1)对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1>0;
(2)m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
(3)已知回归直线的斜率的值为1.23,样本点的中心为(4,5),则回归直线方程为
=1.23x+0.08
(4)若实数x,y∈[-1,1],则满足x2+y2≥1的概率为
.
(1)对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1>0;
(2)m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
(3)已知回归直线的斜率的值为1.23,样本点的中心为(4,5),则回归直线方程为
| ? |
| y |
(4)若实数x,y∈[-1,1],则满足x2+y2≥1的概率为
| π |
| 4 |
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:综合题
分析:(1)中,由命题p写出它的否定¬p,判定命题(1)是否正确;
(2)中,求出直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直时,m的取值,即可判定命题(2)是否正确;
(3)中,由回归直线过样本中心点,求出回归直线方程,即可判定命题(3)是否正确;
(4)中,画出图形,根据图形求出满足条件的概率,判定命题(4)是否正确.
(2)中,求出直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直时,m的取值,即可判定命题(2)是否正确;
(3)中,由回归直线过样本中心点,求出回归直线方程,即可判定命题(3)是否正确;
(4)中,画出图形,根据图形求出满足条件的概率,判定命题(4)是否正确.
解答:
 解:对于(1),命题p:?x∈R,使得x2+x+1<0的否定是¬p:?x∈R,均有x2+x+1≥0;∴命题(1)错误.
解:对于(1),命题p:?x∈R,使得x2+x+1<0的否定是¬p:?x∈R,均有x2+x+1≥0;∴命题(1)错误.
对于(2),∵直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直时,m(m+3)-6m=0,即m=0或m=3,∴m=3不是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;∴(2)错误.
对于(3),∵回归直线
=bx+a的斜率的值为1.23,直线过样本点的中心(4,5),∴a=0.08,
∴回归直线方程是
=1.23x+0.08;命题(3)正确.
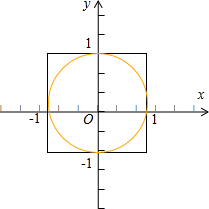
对于(4),如图,;
当实数x,y∈[-1,1]时,则满足x2+y2≥1的概率
;∴命题(4)错误.
综上,以上正确的命题是(3);
故选:A.
 解:对于(1),命题p:?x∈R,使得x2+x+1<0的否定是¬p:?x∈R,均有x2+x+1≥0;∴命题(1)错误.
解:对于(1),命题p:?x∈R,使得x2+x+1<0的否定是¬p:?x∈R,均有x2+x+1≥0;∴命题(1)错误.对于(2),∵直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直时,m(m+3)-6m=0,即m=0或m=3,∴m=3不是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;∴(2)错误.
对于(3),∵回归直线
 |
| y |
∴回归直线方程是
| ? |
| y |
对于(4),如图,;
当实数x,y∈[-1,1]时,则满足x2+y2≥1的概率
| 4-π |
| 4 |
综上,以上正确的命题是(3);
故选:A.
点评:本题通过命题真假的判定,考查了命题的否定、充分与必要条件、回归直线方程以及几何概率的知识,解题时应对每一个命题认真分析,以便作出正确的选择,是综合性题目.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”.下列函数中,有“巧值点”的是( )
①f(x)=x2;
②f(x)=e-x;
③f(x)=lnx;
④f(x)=
.
①f(x)=x2;
②f(x)=e-x;
③f(x)=lnx;
④f(x)=
| 1 |
| x |
| A、①③④ | B、③ | C、②③ | D、②④ |
若曲线y=x2上存在点(x,y)满足约束条件
,则实数m的取值范围是( )
|
| A、[-2,1] |
| B、[1,+∞) |
| C、(0,+∞) |
| D、(-∞,1) |
焦距是8,离心率0.8的椭圆的标准方程为( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、以上都不是 |
式子a
-b
的最大值为( )
| 1-b2 |
| 1-a2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
已知等差数列{an}中,a2=6,前7项和S7=84,则a6等于( )
| A、18 | B、20 | C、24 | D、32 |
在复平面内,复数
(i是虚数单位)所对应的点位于( )
| 2-3i |
| 3+4i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |