题目内容
1.函数f(x)=asinx-bcosx图象的对称轴方程是x=$\frac{π}{4}$,则直线ax-by+c=0的斜率为-1.分析 当x取值为对称轴时,函数取值为最大或最小,得到a+b=0,由此能求出直线ax-by+c=0的斜率.
解答 解:当x取值为对称轴时,函数取值为最大或最小.
即:|$\frac{a-b}{\sqrt{2}}$|=$\sqrt{{a}^{2}{+b}^{2}}$,解得:a+b=0.
∴直线ax-by+c=0的斜率k=$\frac{a}{b}$=-1,
故答案为:-1.
点评 本题考查直线的斜率问题,考查计算能力,转化思想的应用,解题时要认真审题.

练习册系列答案
相关题目
9.已知1<a≤3,-2<b≤5,则2b-a的取值范围是( )
| A. | (-7,9) | B. | (-4,7) | C. | [-7,9] | D. | [-4,7] |
6.已知a=logπe,b=($\sqrt{6}$)-2,c=$\frac{1}{ln2}$,则a,b,c的大小关系为( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | a>c>b |
1.已知两条直线l1:x+2ay-1=0,l2:2x-5y=0,且l1⊥l2,则满足条件a的值为( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | -5 | D. | 5 |
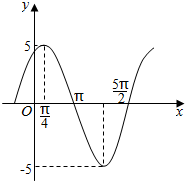 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).