题目内容
已知圆C:x2+y2-4x-8y+16=0,
(1)过点A(-4,2)的直线l被圆C截得弦长为2
,求l的方程;
(2)已知A(-4,m),m>0,P为x轴上的点,Q(x,y)为圆C上的点,若|AP|+|PQ|的最小值为8,求m的值.
(1)过点A(-4,2)的直线l被圆C截得弦长为2
| 2 |
(2)已知A(-4,m),m>0,P为x轴上的点,Q(x,y)为圆C上的点,若|AP|+|PQ|的最小值为8,求m的值.
考点:直线和圆的方程的应用
专题:计算题,直线与圆
分析:(1)设出直线的点斜式方程,化为一般式,求出圆心到直线的距离,再由弦长公式2
,即可求出斜率,即可得到直线方程;
(2)求出A关于x轴的对称点B的坐标,可得|PA|+|PQ|的最小值是|BC|-r,即可求出m.
| r2-d2 |
(2)求出A关于x轴的对称点B的坐标,可得|PA|+|PQ|的最小值是|BC|-r,即可求出m.
解答:
 解:(1)圆C:x2+y2-4x-8y+16=0,即(x-2)2+(y-4)2=4,
解:(1)圆C:x2+y2-4x-8y+16=0,即(x-2)2+(y-4)2=4,
则圆心C(2,4),半径r=2.
设直线l的方程为:x=-4或y-2=k(x+4),
当x=-4,则有圆心到直线的距离大于半径,故不成立;
直线l的一般式:kx-y+2+4k=0,
由弦长公式:2
=2
=2
,
则d=
.
则
=
,解得k=
,
则直线l的方程为:(6+
)x-17y+58+4
=0或
(6-
)x-17y+58-4
=0;
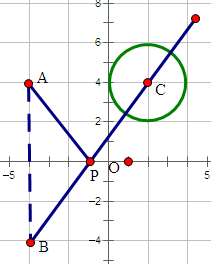
(2)设A(-4,m)关于x轴的对称点为B(-4,-m),
则|PA|+|PQ|≥|BP|+|PC|-r,即最小值是|BC|-r
=
-2=8.
解得m=4.
 解:(1)圆C:x2+y2-4x-8y+16=0,即(x-2)2+(y-4)2=4,
解:(1)圆C:x2+y2-4x-8y+16=0,即(x-2)2+(y-4)2=4,则圆心C(2,4),半径r=2.
设直线l的方程为:x=-4或y-2=k(x+4),
当x=-4,则有圆心到直线的距离大于半径,故不成立;
直线l的一般式:kx-y+2+4k=0,
由弦长公式:2
| r2-d2 |
| 4-d2 |
| 2 |
则d=
| 2 |
则
| |2k-4+2+4k| | ||
|
| 2 |
6±
| ||
| 17 |
则直线l的方程为:(6+
| 19 |
| 19 |
(6-
| 19 |
| 19 |
(2)设A(-4,m)关于x轴的对称点为B(-4,-m),
则|PA|+|PQ|≥|BP|+|PC|-r,即最小值是|BC|-r
=
| (2+4)2+(4+m)2 |
解得m=4.
点评:本题考查直线和圆的方程的应用,考查直线和圆相交的弦长公式,点关于直线的对称点,考查学生的计算能力,求出A关于x轴的对称点B的坐标是关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
在(1-2
+x)6的展开式中,x4的系数是( )
| x |
| A、435 | B、455 |
| C、475 | D、495 |