题目内容
已知A，B为两个定点，动点M到A与B的距离比为常数λ，求点M的轨迹方程，并注明轨迹是什么曲线．
考点：轨迹方程
专题：计算题,直线与圆
分析：设点M（x，y）是曲线上的任意一点，欲求出动点M的轨迹方程，只须求出x，y的关系式即可，结合距离的比，用坐标来表示距离，利用两点间的距离公式化简即可求得点P的轨迹方程．
解答：
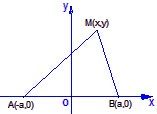解：建立坐标系如图所示，设|AB|=2a，则A（-a，0），B（a，0）．设M（x，y）是轨迹上任意一点．
则由题设，得
=λ，坐标代入，得
=λ，化简得
（1-λ2）x2+（1-λ2）y2+2a（1+λ2）x+（1-λ2）a2=0
（1）当λ=1时，即|MA|=|MB|时，点M的轨迹方程是x=0，点M的轨迹是直线（y轴）．
（2）当λ≠1时，点M的轨迹方程是x2+y2+
x+a2=0，点M的轨迹是以（-
，0）为圆心，
为半径的圆．
解：建立坐标系如图所示，设|AB|=2a，则A（-a，0），B（a，0）．设M（x，y）是轨迹上任意一点．则由题设，得
| |MA| |
| |MB| |
| ||
|
（1-λ2）x2+（1-λ2）y2+2a（1+λ2）x+（1-λ2）a2=0
（1）当λ=1时，即|MA|=|MB|时，点M的轨迹方程是x=0，点M的轨迹是直线（y轴）．
（2）当λ≠1时，点M的轨迹方程是x2+y2+
| 2a(1+λ2) |
| 1-λ2 |
| a(1+λ2) |
| 1-λ2 |
| 2aλ |
| |1-λ2| |
点评：本题考查轨迹方程，利用的是直接法，直接法是将动点满足的几何条件或者等量关系，直接坐标化，列出等式化简即得动点轨迹方程．
练习册系列答案
相关题目
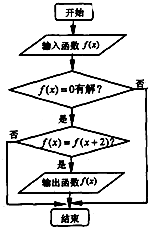
运行如图所示的程序框图，输入下列四个函数，则可以输出的函数是（ ）
| A、f（x）=x2 | ||
B、f（x）=cos（
| ||
| C、f（x）=tanx | ||
| D、f（x）=sin（πx） |
适合方程2z-|z|-i=0的复数z是（ ）
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、±
|
如果角θ的终边经过点P（-
，
），那么tanθ等于（ ）
| ||
| 2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|