题目内容
如图K457所示,在直棱柱ABCD A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.
(1)证明:AC⊥B1D;
(2)求直线B1C1与平面ACD1所成角的正弦值.

解:方法一:(1)证明:因为BB1⊥平面ABCD,AC⊂平面ABCD,所以AC⊥BB1.
又AC⊥BD,且BB1∩BD=B,所以AC⊥平面BB1D.
因为B1D⊂平面BB1D,所以AC⊥B1D.

(2)因为B1C1∥AD,所以直线B1C1与平面ACD1所成的角等于直线AD与平面ACD1所成的角(记为θ).
如图所示,连接A1D.
因为棱柱ABCD A1B1C1D1是直棱柱,且∠B1A1D1=∠BAD=90°,
所以A1B1⊥平面ADD1A1,所以A1B1⊥AD1.
又AD=AA1=3,所以四边形ADD1A1是正方形,于是A1D⊥AD1.又A1D∩A1B1=A1,
所以AD1⊥平面A1B1D,于是AD1⊥B1D.
由(1)知,AC⊥B1D,且AD1∩AC=A,
所以B1D⊥平面ACD1,
故∠ADB1=90°-θ.
在直角梯形ABCD中,因为AC⊥BD,所以∠BAC=∠ADB,
从而Rt△ABC∽Rt△DAB,故 =
= ,
,
即AB= =
= .
.
连接AB1,易知△BB1D是直角三角形,且B1D2=BB +BD2=BB
+BD2=BB +AB2+AD2=21,即B1D=
+AB2+AD2=21,即B1D= ,
,
所以在Rt△AB1D中,cos∠ADB1= =
= =
= ,
,
即cos(90°-θ)= ,从而可得sin θ=
,从而可得sin θ= ,
,
即直线B1C1与平面ACD1所成角的正弦值为 .
.
方法二:(1)证明:易知,AB,AD,AA1两两垂直.如图所示,以A为坐标原点,AB,AD,AA1所在直线分别为x轴、y轴、z轴建立空间直角坐标系.设AB=t,则有A(0,0,0),B(t,0,0),B1(t,0,3),C(t,1,0),C1(t,1,3),D(0,3,0),D1(0,3,3),

 令x=1,则n=(1,-
令x=1,则n=(1,- ,
, ).
).
设直线B1C1与平面ACD1所成的角为θ,则
 即直线B1C1与平面ACD1所成角的正弦值为
即直线B1C1与平面ACD1所成角的正弦值为 .
.

 阅读快车系列答案
阅读快车系列答案
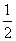 ,y=-
,y=- ,y=-
,y=-

 B.
B. C.
C. D.
D.
 B.
B.
 C.
C.

 对一切
对一切 恒成立,则实数
恒成立,则实数 取值的集合为( )
取值的集合为( ) B.
B. C.
C. D.
D.
 的解集为
的解集为 ,则不等式
,则不等式 的解集为( )
的解集为( ) B.
B. 或
或
 D.
D. 或
或