题目内容
9.一位同学家里订了一份报纸,送报人每天早上6:20-7:40之间将报纸送达,该同学需要早上7:00-8:00之间出发上学,则这位同学在离开家之前能拿到报纸的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
分析 设送报人到达的时间为x,这位同学在离开家为y,(x,y)可以看成平面中的点,
利用图形表示出事件所构成的区域,利用面积比求出对应的概率值.
解答 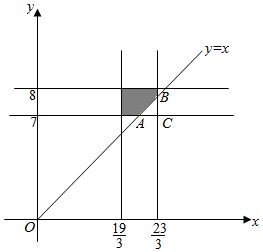 解:如图所示,设送报人到达的时间为x,这位同学在离开家为y;
解:如图所示,设送报人到达的时间为x,这位同学在离开家为y;
则(x,y)可以看成平面中的点,试验的全部结果所构成的区域为
Ω={(x,y)|$\frac{19}{3}$≤x≤$\frac{23}{3}$,且7≤y≤8},
其矩形区域的面积为SΩ=($\frac{23}{3}$-$\frac{19}{3}$)×(8-7)=$\frac{4}{3}$;
事件A所构成的区域为
A={(x,y)|$\frac{19}{3}$≤x≤$\frac{23}{3}$,且7≤y≤8,且x≤y},
即图中的阴影部分,
其中A(7,7),C($\frac{23}{3}$,7),B($\frac{23}{3}$,$\frac{23}{3}$),
且△ABC的面积为S′=$\frac{1}{2}$×($\frac{23}{3}$-7)×($\frac{23}{3}$-7)=$\frac{2}{9}$,
则阴影部分的面积为SA=$\frac{4}{3}$-$\frac{2}{9}$=$\frac{10}{9}$.
所求对应的概率为P=$\frac{\frac{10}{9}}{\frac{4}{3}}$=$\frac{5}{6}$.
故选:D.
点评 本题考查了几何概型的概率计算问题,也考查了二元一次不等式组表示平面区域的问题,是中档题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
7.已知a=0.92,b=20.9,c=log20.9,则a,b,c的大小关系为( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
14.已知tan95°=k,则tan35°=( )
| A. | $\frac{\sqrt{3}-k}{1+\sqrt{3}k}$ | B. | $\frac{k+\sqrt{3}}{1+\sqrt{3}k}$ | C. | $\frac{k+\sqrt{3}}{1-\sqrt{3}k}$ | D. | $\frac{k-\sqrt{3}}{1+\sqrt{3}k}$ |
1.设M为△ABC所在平面内一点,$\overrightarrow{BC}$=2$\overrightarrow{CM}$,且$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则$\frac{μ}{λ}$=( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 4 |
 已知函数f(x)=sin(ωx+φ)(ω>0)的部分图如图所示,下面结论正确的是( )
已知函数f(x)=sin(ωx+φ)(ω>0)的部分图如图所示,下面结论正确的是( )


