Question

8．在平面直角坐标系中，圆C的参数方程为$\left\{\begin{array}{l}{x=2（1+cosα）}\\{y=2sinα}\end{array}$（α为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，已知点P的极坐标为（ρ₀，$\frac{π}{2}$）．
（1）求圆C的极坐标方程；
（2）过点P作圆C的切线，切点分别为A，B两点，且∠APB=120°，求ρ₀．

Answer 1

分析 （1）先求出圆的普通方程，再转化为极坐标方程；（2）结合图象求出PA的长，从而求出ρ₀的值即可．

解答 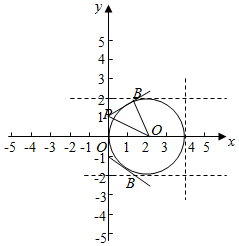解：（1）圆的普通方程为（x-2）²+y²=4，即x²+y²-4x=0，
∴圆C的极坐标方程为ρ²-4ρcosθ=0，即ρ=4cosθ．
（2）已知点P的极坐标为（ρ₀，$\frac{π}{2}$），
故P在y轴上，
画出圆在直角坐标系中的图象，如图所示：
，
若P在y轴的上方，由∠APB=120°，
得∠AOP=30°，则tan∠AOP=$\frac{AP}{OA}$=$\frac{AP}{2}$=$\frac{\sqrt{3}}{3}$，
解得：AP=$\frac{2\sqrt{3}}{3}$，
故ρ₀=$\frac{2\sqrt{3}}{3}$，
若P在y轴的下方，则ρ₀=-$\frac{2\sqrt{3}}{3}$．

点评 本题考查了参数方程，极坐标方程与普通方程的转化，考查数形结合思想，属于中档题．