题目内容
已知F是抛物线y2=2px(p>0)的焦点,点M(4,2),P是抛物线上的任意一点,|PM|+|PF|的最小值为5.
(1)求该抛物线的方程;
(2)设过点F,斜率为1的直线与抛物线交于A、B两点,当|PM|+|PF|取得最小值时,求:
①△PAB的面积;
②△AOB(O是坐标原点)外接圆的方程.
(1)求该抛物线的方程;
(2)设过点F,斜率为1的直线与抛物线交于A、B两点,当|PM|+|PF|取得最小值时,求:
①△PAB的面积;
②△AOB(O是坐标原点)外接圆的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件得4+
=5,由此能求出抛物线的方程.
(2)①当|PM|+|PF|取得最小值时,点P为过M点且垂直于准线的直线与抛物线的交点,从而P(1,2),过点F(1,0)斜率为1的直线方程为y=x-1,由
,得x2-6x+1=0,由此椭圆弦长公式和点到直线的距离公式能求出△PAB的面积.
②解方程x2-6x+1=0,得A(3+2
,2+2
),B(3-2
,2-2
),从而AB有中垂线的方程为x+y-5=0,OA的中垂线方程为:y-(1+
)=(-
-
)(x-
-
),由此能示出△AOB外接圆方程.
| p |
| 2 |
(2)①当|PM|+|PF|取得最小值时,点P为过M点且垂直于准线的直线与抛物线的交点,从而P(1,2),过点F(1,0)斜率为1的直线方程为y=x-1,由
|
②解方程x2-6x+1=0,得A(3+2
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 2 |
解答:
解:(1)∵抛物线上的点到焦点距离=到准线的距离,
∴|PM|+|PF|=|PM|+P到准线的距离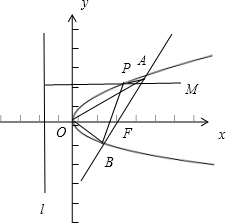
≤M到到准线的距离
=4+
=5,
解得p=2,∴抛物线的方程y2=4x.
(2)①当|PM|+|PF|取得最小值时,
点P为过M点且垂直于准线的直线与抛物线的交点,
∴P(xP,2),∴22=4xP,解得xP=1,
∴P(1,2),
过点F(1,0)斜率为1的直线方程为y=x-1,
由
,得x2-6x+1=0,
△=36-4=32>0,设A(x1,y1),B(x2,y2),
x1+x2=6,x1x2=1,
∴|AB|=
=8,
点P(1,2)到直线AB:y=x-1的距离d=
=
,
∴△PAB的面积S△PAB=
×
×8=4
.
②解方程x2-6x+1=0,得x1=3+2
,x2=3-2
,
∴A(3+2
,2+2
),B(3-2
,2-2
),
∴AB的中点坐标为(3,2),
kAB=
=1,∴AB有中垂线的方程为:y-2=-(x-3),即x+y-5=0.①
OA有中点(
+
,1+
),kOA=
=2
-2,
∴OA的中垂线方程为:y-(1+
)=(-
-
)(x-
-
),②
联立①②得△AOB外接圆圆心为:(
,
),
外接圆半径r=
=
,
∴△AOB(O是坐标原点)外接圆的方程:
(x-
)2+(y-
)2=
.
∴|PM|+|PF|=|PM|+P到准线的距离

≤M到到准线的距离
=4+
| p |
| 2 |
解得p=2,∴抛物线的方程y2=4x.
(2)①当|PM|+|PF|取得最小值时,
点P为过M点且垂直于准线的直线与抛物线的交点,
∴P(xP,2),∴22=4xP,解得xP=1,
∴P(1,2),
过点F(1,0)斜率为1的直线方程为y=x-1,
由
|
△=36-4=32>0,设A(x1,y1),B(x2,y2),
x1+x2=6,x1x2=1,
∴|AB|=
| (1+1)(36-4) |
点P(1,2)到直线AB:y=x-1的距离d=
| |1-2-1| | ||
|
| 2 |
∴△PAB的面积S△PAB=
| 1 |
| 2 |
| 2 |
| 2 |
②解方程x2-6x+1=0,得x1=3+2
| 2 |
| 2 |
∴A(3+2
| 2 |
| 2 |
| 2 |
| 2 |
∴AB的中点坐标为(3,2),
kAB=
4
| ||
4
|
OA有中点(
| 3 |
| 2 |
| 2 |
| 2 |
1+
| ||||
|
| 2 |
∴OA的中垂线方程为:y-(1+
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 2 |
联立①②得△AOB外接圆圆心为:(
7+8
| ||
| 2 |
3-8
| ||
| 2 |
外接圆半径r=
(
|
|
∴△AOB(O是坐标原点)外接圆的方程:
(x-
7+8
| ||
| 2 |
3-8
| ||
| 2 |
161+16
| ||
| 2 |
点评:本题考查抛物线方程的求法,考查三角形面积的求法,考查三角形外接圆方程的求法,解题时要认真审题,注意椭圆弦长公式的合理运用.

练习册系列答案
相关题目
 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求: