题目内容
7.已知函数$f(x)=\left\{\begin{array}{l}sin(πx)(x∈[{-2,0}])\\{3^{-x}}+1\;(x>0)\end{array}\right.$,则y=f[f(x)]-4的零点为( )| A. | $-\frac{π}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{3}{2}$ | D. | $-\frac{1}{2}$ |
分析 当x>0时,y=f[f(x)]-4的零点即方程f[f(x)]-4=0的根,3-f(x)+1=4;即可求得f(x)=-1,当x∈[-2,0]时,sin(-πx)=-1,即可求得x的值.
解答 解:y=f[f(x)]-4的零点即方程f[f(x)]-4=0的根,
故3-f(x)+1=4;
解得:f(x)=-1,
当x∈[-2,0]时,
sin(πx)=-1,πx=-$\frac{π}{2}$+2kπ,(k∈Z)x=-$\frac{1}{2}$+2k,(k∈Z),
∴x=-$\frac{1}{2}$;
故选D.
点评 本题考查了分段函数的定义及函数的零点与方程的根的联系,属于基础题.

练习册系列答案
相关题目
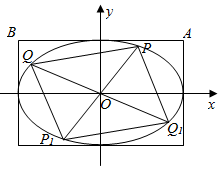 已知椭圆C的中心在原点,对称轴为坐标轴,左焦点为F1(-1,0),离心率为$\frac{1}{2}$.
已知椭圆C的中心在原点,对称轴为坐标轴,左焦点为F1(-1,0),离心率为$\frac{1}{2}$.