题目内容
12.求方程(sinx+cosx)tanx=2cosx在区间(0,π)上的解.分析 “切化弦”的思想,利用二倍角和辅助角公式化简,即可求方程.
解答 解:(sinx+cosx)tanx=2cosx,
即:(sinx+cosx)$\frac{sinx}{cosx}$=2cosx
?sin2x+sinxcosx=2cos2x
?$\frac{1}{2}-\frac{1}{2}$cos2x+$\frac{1}{2}$sin2x=1+cos2x
?sin2x-3cos2x=1
?$\sqrt{10}$sin(2x-θ)=1,θ=arctan3.
?sin(2x-θ)=$\frac{\sqrt{10}}{10}$,
2x-θ=arcsin$\frac{\sqrt{10}}{10}$或2x-θ=π-arcsin$\frac{\sqrt{10}}{10}$,
故得x=$\frac{1}{2}$(arctan3+arcsin$\frac{\sqrt{10}}{10}$)或x=$\frac{1}{2}$(π-arcsin$\frac{\sqrt{10}}{10}$+arctan3)
点评 本题考查了“切化弦”的思想和二倍角和辅助角公式化简计算能力.属于中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
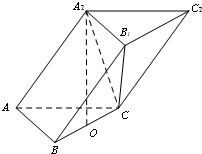 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=$\sqrt{5}$,BC=4,BC的中点为O,A1O垂直于底面ABC.
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=$\sqrt{5}$,BC=4,BC的中点为O,A1O垂直于底面ABC.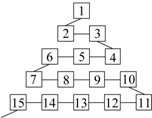 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第7个数是2010.
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第7个数是2010.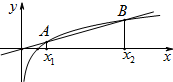 如图,过原点斜率为k的直线与曲线y=lnx交于两点A(x1,y1),B(x2,y2)
如图,过原点斜率为k的直线与曲线y=lnx交于两点A(x1,y1),B(x2,y2)