题目内容
7.3x+4y+5z=10,x2+y2+z2的最小值为2.分析 利用题中条件:“3x+4y+5z=10”构造柯西不等式:(x2+y2+z2)×(9+16+25 )≥(3x+4y+5z)2这个条件进行计算即可.
解答 证明:(x2+y2+z2)×(9+16+25 )≥(3x+4y+5z)2=100
∴x2+y2+z2≥2,
则x2+y2+z2的最小值为2,
故答案为:2.
点评 本题考查柯西不等式,关键是利用(x2+y2+z2)×(9+16+25 )≥(3x+4y+5z)2.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
16.设函数f(x)在R上存在导数f′(x),?x∈R,有f(-x)+f(x)=2x2,在(0,+∞)上f′(x)>2x,若f(2-m)+4m-4≥f(m),则实数m的取值范围为( )
| A. | -1≤m≤1 | B. | m≤1 | C. | -2≤m≤2 | D. | m≥2 |
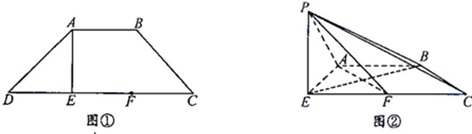
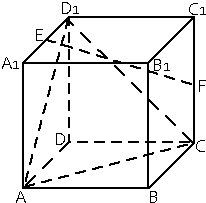 如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.
如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.