题目内容
6.已知复数z=(2+i)m2-$\frac{6m}{1-i}-2({1-i})({m∈R})$.(1)当实数m取什么值时,复数z是纯虚数;
(2)若z在复平面内对应的点在第二、四象限角平分线上,求|z|.
分析 (1)z=(2+i)m2-3m(1+i)-2(1-i)=(2m2-3m-2)+(m2-3m+2)i,当实部等于0,虚部不等于0时,列出方程组,求解即可得答案;
(2)当2m2-3m-2=-(m2-3m+2),即m=0或m=2时,z为复平面内第二、第四象限角平分线上的点对应的复数,分类当m=0和m=2时,求出|z|即可.
解答 解:z=(2+i)m2-3m(1+i)-2(1-i)=(2m2-3m-2)+(m2-3m+2)i,
(1)当$\left\{\begin{array}{l}{2{m}^{2}-3m-2=0}\\{{m}^{2}-3m+2≠0}\end{array}\right.$,即 $m=-\frac{1}{2}$时,z为纯虚数;
(2)当2m2-3m-2=-(m2-3m+2),即m=0或m=2时,z为复平面内第二、第四象限角平分线上的点对应的复数,
若m=0,$z=-2+2i,|z|=2\sqrt{2}$,
若m=2,z=0,|z|=0,
∴$|z|=2\sqrt{2}$或|z|=0.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17.如果随机变量ξ~B(n,p),且E(ξ)=10,D(ξ)=8,则p等于( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
14.定义在(-1,1)上的函数f(x)满足:$f(x)-f(y)=f({\frac{x-y}{1-xy}})$,当x∈(-1,0)时,有f(x)>0,且$f({-\frac{1}{2}})=1$.设$m=f({\frac{1}{5}})+f({\frac{1}{11}})+…+f({\frac{1}{{{n^2}+n-1}}}),\;\;n≥2,n∈{N^*}$,则实数m与-1的大小关系为( )
| A. | m<-1 | B. | m=-1 | C. | m>-1 | D. | 不确定 |
11.下列说法错误的是( )
| A. | 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 | |
| B. | 在线性回归分析中,回归直线不一定过样本点的中心($\overline{x}$,$\overline{y}$) | |
| C. | 在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 | |
| D. | 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 |
9.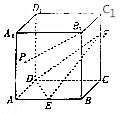 如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
 如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )| A. | [$\frac{1}{2}$,$\frac{3}{2}$] | B. | [0,1] | C. | [$\frac{1}{3}$,$\frac{\sqrt{10}}{3}$] | D. | [$\frac{1}{3}$,$\frac{\sqrt{13}}{3}$] |
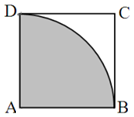 已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.
已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.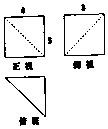 某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.
某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.